图解队列

引言

这篇文章是根据我学习 queue 的学习笔记总结而成的。

定义

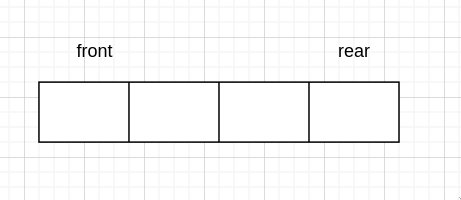
queue 是线性表(linear list)中的一种，元素间遵循一对一的原则。

除此外，queue 遵循 FIFO(first in first out) 原则，即先进的元素先出。

分类

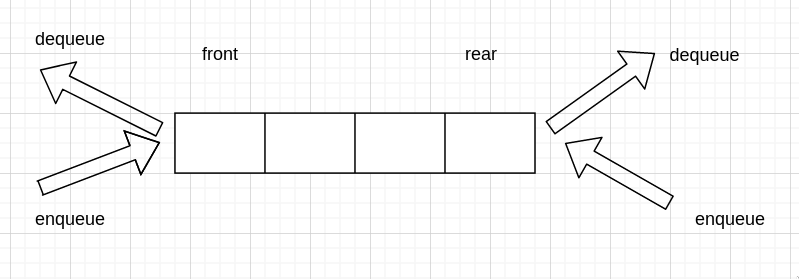
queue 入队和出队方式分为单端队列和双端队列，一般我们说队列都指的是单端队列。

单端队列就是只能在队尾（rear) 入队，只能在队首(front)出队的队列

双端队列则是队首和队尾都可以入队和出队的队列。(deque)(double-ended queue)

queue 按照入出队元素的选择方式分为普通队列的和优先队列。

普通的队列就是按顺序入出队，入队到队尾，把队首出队。

而优先队列则要看优先级，优先级是自己定的，每个元素都有其优先级，而入出队则选择最大或最小优先级的元素来操作。

优先队列分为有序的和无序的，如果优先级是指最大值，每次出队都是取出最大值。那么就分为两类，入队时不排序，直接存在队尾，而出队时则需要搜索，取出最大值，这样入队时间复杂度为 O(1), 而出队的时间复杂度为 O(n), 类似的，如果是入队时排序，那么在入队时就要插入到对应位置，而出队时则直接出队首的位置，入队的时间复杂度为 O(n), 出队为 O(1), 这其中还设计搜索算法和排序算法。

没有特别说明是双端队列和或优先队列时，都是默认的指单端普通队列。

应用的比较广的单端普通队列，也是我们生活中比较常见的，如实际生活中的排队，不考虑插队这种情况的话，也是队尾入队，队首出队，你可以观察一下生活中遇到的队伍是不是这样。

实现

queue 可以用 顺序存储 或 链式存储实现。 无论哪种方式都需要用两个指针，front 和 rear 指向 queue 首和 queue 尾

顺序存储

首先定义 queue，需要两指针和数据域

// 分配的内存大小
#define SIZE 5

// 定义 queue
typedef struct {
    int data[SIZE];  //数据
    int front;       // 首指针
    int rear;        //尾指针
} Queue;

然后初始化，两指针同时指向 array[0] 处，因为 0 处是初始位置比较容易管理

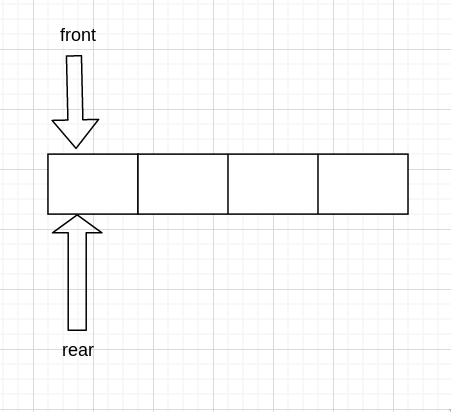
// 初始化 queue
Queue CreateQueue() {
    Queue queue;
    queue.rear = 0;
    queue.front = 0;
    return queue;
}

现在问题来了， 0 处设置为 队首还是队尾呢？从技术上来说，肯定都是能够实现的，但是问题是，哪个更适合呢？

0 处为队首

现在我们假设 0 处是队首, 只能从队尾入队，从队首出队 假设队伍现在是这样的

入队

我们发现现在的尾指针指向的值是空的，也就是说，尾指针其实指向的是实际队尾的下一个

那么要入队，队列又只能从队尾入队，所以直接给尾指针指向的赋值

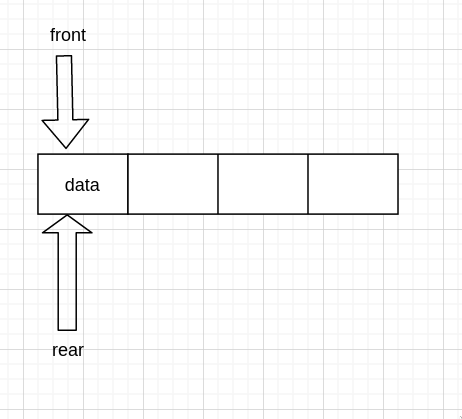
然后尾指针需要向后移动一次

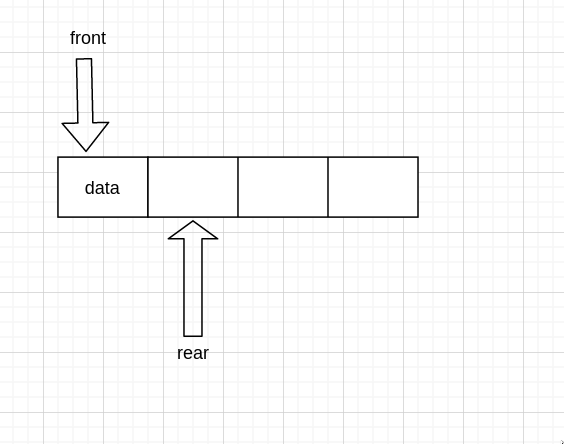
转换为代码

// 入队
void EnQueue(Queue *queue, int data) {
    // 先尾指针赋值
    queue->data[queue->rear] = data;
    // 再尾指针移动
    queue->rear++;
}

需要注意如果 queue 已经满了，入队会 overflow，所以还需要先判断是不是满了

问题是怎么判断是不错满了呢？

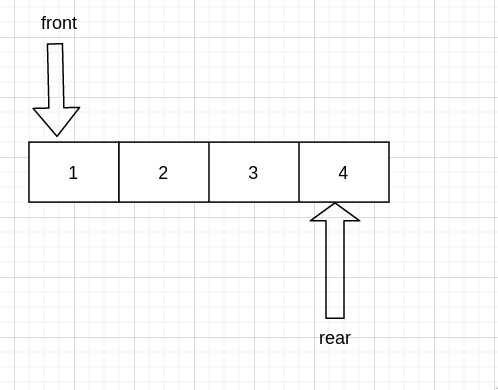
在 array 中，满了的意思是分配的内存不能再给 queue 用了，所以就是 rear 指向分配内存的边缘了，所以只需要判断 rear 是不是等于 SIZE 即可

// 入队
void EnQueue(Queue *queue, int data) {
    // 判断是否 overflow
    if (queue->rear == SIZE) {
        return;
    }

    // 先尾指针赋值
    queue->data[queue->rear] = data;
    // 再尾指针移动
    queue->rear++;
}

出队

现在假设 queue 是这样的

要出队的话，只需要首指针向右移动一次即可

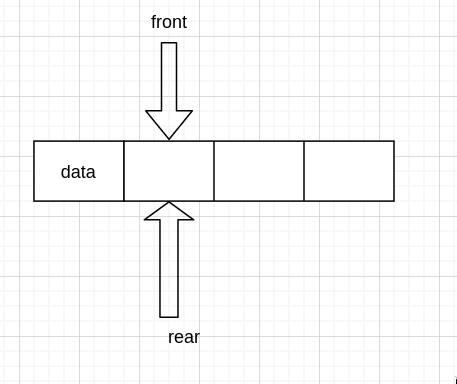
可能有人会问，那出队的那个内存的值怎么办呢？

一般 queue 作为局部变量的话，用 array 来实现，都是分配在 stack 上的，调用函数时系统自动分配，函数结束自动回收。而一般分配后，也不会清空，刚分配的内存存的值也是不能确定的脏值。并且，我们操作 queue 只看的是 front 和 rear 中间的部分，所以那个值没有改变的必要。

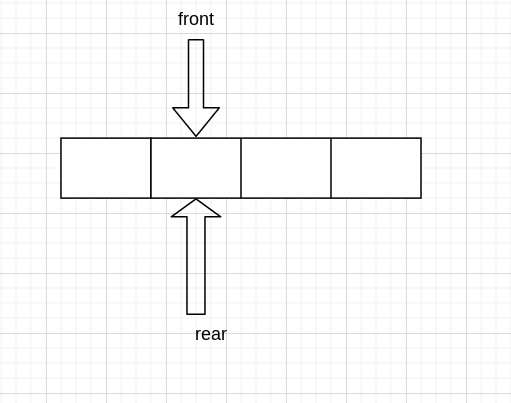
用代码来实现

// 出队
void DeQueue(Queue *queue) {
    // 首指针移动
    queue->front++;
}

同样的，不要忘记判断边界条件，如果已经是空 queue 的话，再出队会 underflow，所以还需要判断是否为空。

要判断是否为空比较容易理解，只需判断 front 是否等于 rear 即可

// 出队
void DeQueue(Queue *queue) {
    // 判断是否为空
    if (queue->rear == queue->front) {
        return;
    }
    // 首指针移动
    queue->front++;
}

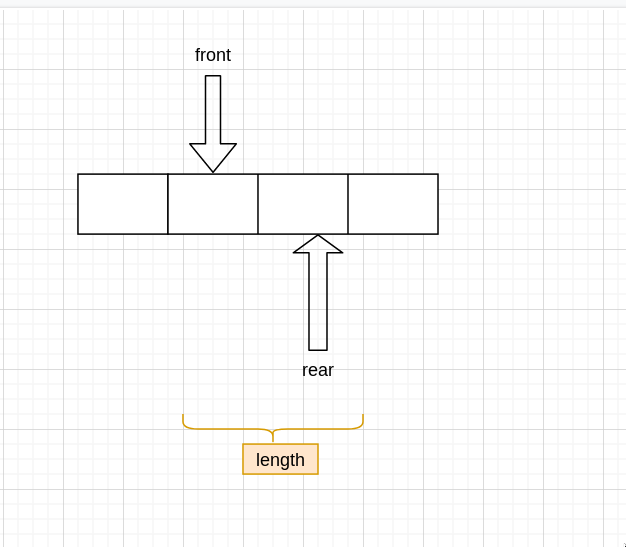
获取队伍长度

要获取队伍长度的话，只需要得到 rear 和 front 间的长度即可，也不用判断是否为空，为空是长度为 0

// 获取 queue 长度
int Len(Queue *queue) {
    return queue->rear - queue->front;
}

0 处为队尾

现在我们假设队伍是这样的

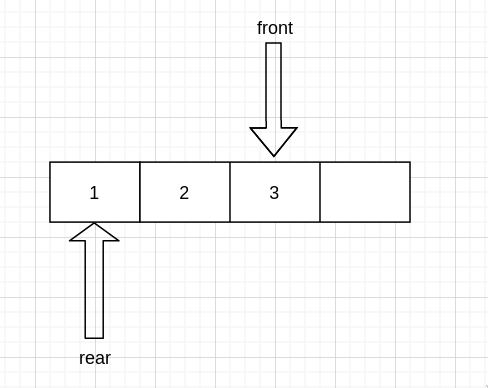
入队

入队的话，需要在 rear 处入队，而 rear 在 0 处，左边又没有地方，所以只能往右边存，现在右边又没有空，所以需要右边留一个空出来。这样的话，就需要右边每个值都向右移动一个位置

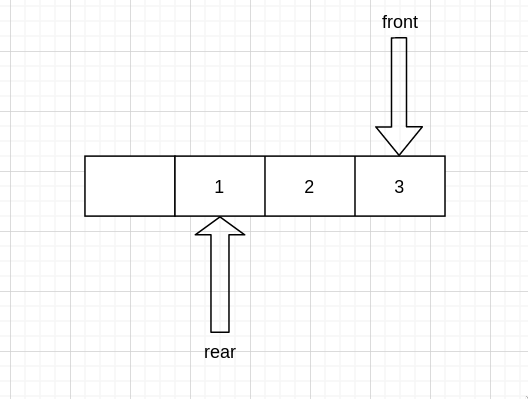
然后 rear 向左移动

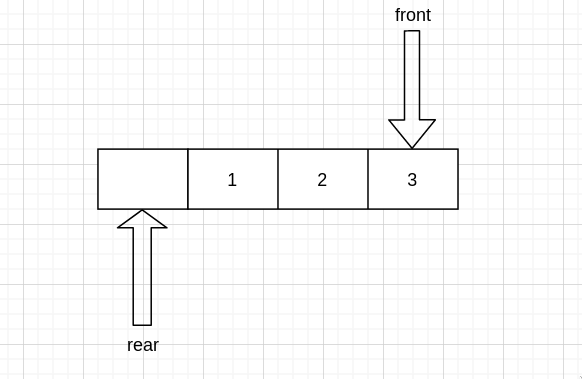
再赋值

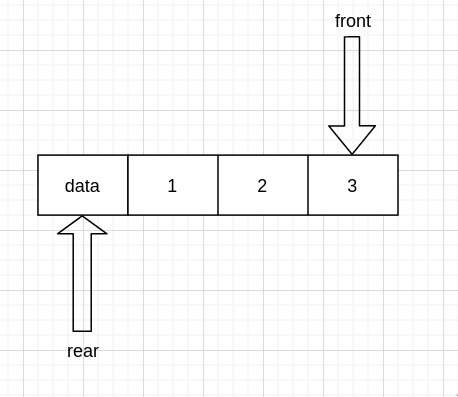
我们发现如果把 0 作为队尾，入队的话，时间复杂度是 O(n), 而把 0 作为队首则都是 O(1), 同样的，按照一般的习惯，队尾一般都比队首大，可是把 0 作为队尾则反过来了，不符合我们的习惯。所以一般还是把 0 处作为队首比较好。

当然有人可能会问，分配一块内存，然后直接在中间某处作为队首队尾如何

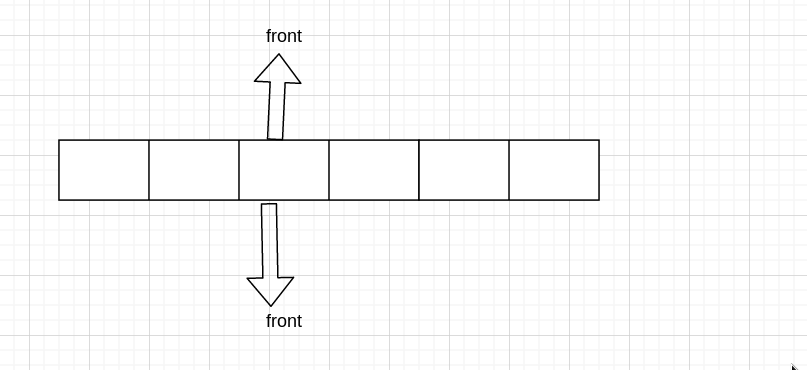
这样的话，无论往哪边排队，都是可以的，不过一般我们没有这样做而已。

实际操作

我们来实际看一下

#include <stdio.h>
#include <stdlib.h>

#define SIZE 5

typedef struct {
    int data[SIZE];
    int front;
    int rear;
} Queue;

Queue CreateQueue() {
    Queue queue;
    queue.rear = 0;
    queue.front = 0;
    return queue;
}

// 入队
void EnQueue(Queue *queue, int data) {
    // 判断是否 overflow
    if (queue->rear == SIZE) {
        return;
    }

    // 先尾指针赋值
    queue->data[queue->rear] = data;
    // 再尾指针移动
    queue->rear++;
}

// 出队
void DeQueue(Queue *queue) {
    // 判断是否为空
    if (queue->rear == queue->front) {
        return;
    }
    // 尾指针移动
    queue->front++;
}

// 获取 queue 长度
int Len(Queue *queue) {
    return queue->rear - queue->front;
}

void TraverseQueue(Queue queue) {
    while (queue.front != queue.rear) {
        printf("%d\n", queue.data[queue.front]);
        queue.front++;
    }
}

int main(void) {
    Queue queue = CreateQueue();
    EnQueue(&queue, 1);
    EnQueue(&queue, 2);
    EnQueue(&queue, 3);
    EnQueue(&queue, 4);
    EnQueue(&queue, 5);

    TraverseQueue(queue);

    DeQueue(&queue);

    TraverseQueue(queue);

    return 0;
}

循环队列

我们现在再来看一下上面，刚开始时队列是这样的

然后入队一次，出队一次，变成了这样

发现没有，队列在往右移动，其实容易理解，入队和出队都是指针往右动，那么队列总体在往右移动也正常，但是左边的那些内存空间呢？

我们会发现随着队列的移动，左边的空间被浪费了，而且越来越多。那么有什么办法重新利用起左边的那些空间吗？

既然队列在往右移动，那么只要往右移动到边界后，又重新移动到左边就行了，这就是一个周期函数，自变量是往右移动的长度，因变量是实际队列的长度

对于用 array 来实现的普通 queue，定义 queue 和初始化都是相同的

// 分配的内存大小
#define SIZE 5

// 定义 queue
typedef struct {
    int data[SIZE];  //数据
    int front;       // 首指针
    int rear;        //尾指针
} Queue;

// 初始化 queue
Queue CreateQueue() {
    Queue queue;
    queue.rear = 0;
    queue.front = 0;
    return queue;
}

所以问题在于，入队和出队

用 array 来实现 queue 时，指针的移动是按下标来实现的，所以只需要指针到达 queue 右边边界后，又等于左边边界下标即可。

入队

同样的，入队时首先给 rear 指向的赋值

然后 rear 移动，当不是循环时，直接向右移动即可，现在循环就不行了。需要先移动，然后对 SIZE 取余数，至于为什么，我们来分析一下

当 rear 没有超过 SIZE 时，移动后取余，还是本身，就等于直接向右移动

当 rear 超过 SIZE 后

再取余，取整就是圈数，取余就是余下的位置

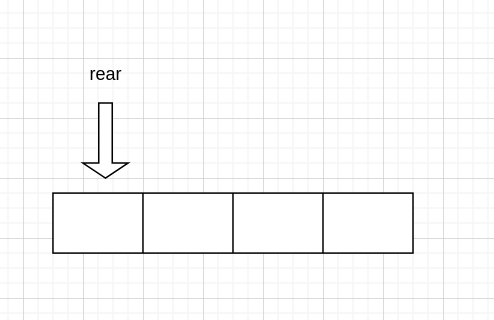
用代码实现

// 入队
void EnQueue(Queue *queue, int data) {
    // 先尾指针赋值
    queue->data[queue->rear] = data;
    // 再尾指针移动
    queue->rear = (queue->rear + 1) % SIZE;
}

同样的，要注意是否 queue 满了，比较尾指针移动后的位置，和 front 的大小

// 入队
void EnQueue(Queue *queue, int data) {
    // 判断是否满 queue 
    if (queue->front == (queue->front + 1) % SIZE) {
        return;
    }

    // 先尾指针赋值
    queue->data[queue->rear] = data;
    // 再尾指针移动
    queue->rear = (queue->rear + 1) % SIZE;
}

出队

假设队伍现在是这样的

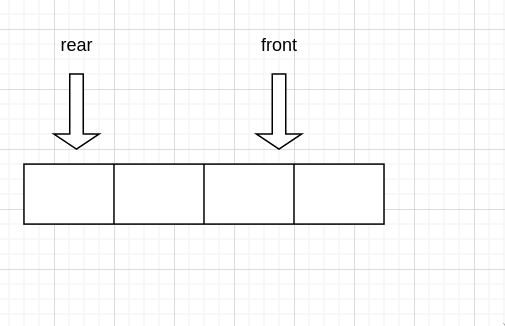
同样的，出队的话，需要 front 向前移动，不过是环上的移动，需要加 1 后取余

// 出队
void DeQueue(Queue *queue) {
    // 尾指针移动
    queue->front = (queue->front + 1) % SIZE;
}

然后要需要是否为空，当为空时，front 等于 rear，直接判断即可，不用移动

// 出队
void DeQueue(Queue *queue) {
    // 判断是否为空
    if (queue->rear == queue->front) {
        return;
    }
    // 尾指针移动
    queue->front = (queue->front + 1) % SIZE;
}

获取长度

// 获取 queue 长度
int Len(Queue queue) {
    return (queue.rear - queue.front + SIZE) % SIZE;
}

实际操作

我们来实际看一下

#include <stdio.h>
#include <stdlib.h>

#define SIZE 5

typedef struct {
    int data[SIZE];
    int front;
    int rear;
} Queue;

Queue CreateQueue() {
    Queue queue;
    queue.rear = 0;
    queue.front = 0;
    return queue;
}

// 入队
void EnQueue(Queue *queue, int data) {
    // 判断是否满 queue
    if (queue->front == (queue->rear + 1) % SIZE) {
        return;
    }

    // 先尾指针赋值
    queue->data[queue->rear] = data;
    // 再尾指针移动
    queue->rear = (queue->rear + 1) % SIZE;
}

// 出队
void DeQueue(Queue *queue) {
    // 判断是否为空
    if (queue->rear == queue->front) {
        return;
    }
    // 尾指针移动
    queue->front = (queue->front + 1) % SIZE;
}

// 获取 queue 长度
int Len(Queue queue) {
    return (queue.rear - queue.front + SIZE) % SIZE;
}

// 遍历 queue
void TraverseQueue(Queue queue) {
    while (queue.front != queue.rear) {
        printf("%d\n", queue.data[queue.front]);
        queue.front++;
    }
}

int main(void) {
    Queue queue = CreateQueue();
    EnQueue(&queue, 1);
    EnQueue(&queue, 2);
    EnQueue(&queue, 3);
    EnQueue(&queue, 4);
    EnQueue(&queue, 5);

    TraverseQueue(queue);

    return 0;
}

我们这时会发现一个问题，明明我们分配了 5 个空间，然后存 5 个值，怎么只得到了 4 个值呢？

我们来实际分析一下，假设已经存到第 3 个值了

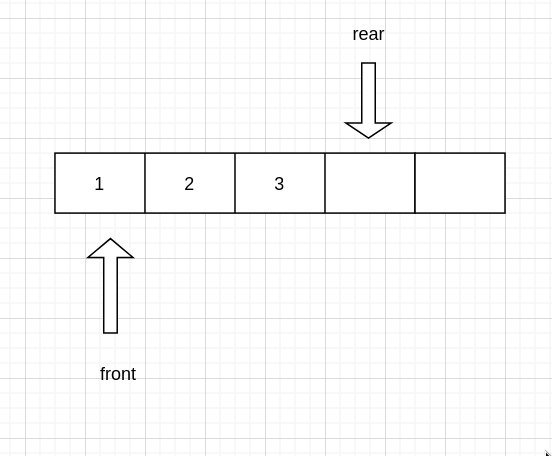
然后入队，queue->front = 0, (queue->rear + 1) % SIZE = 4,没有满，继续

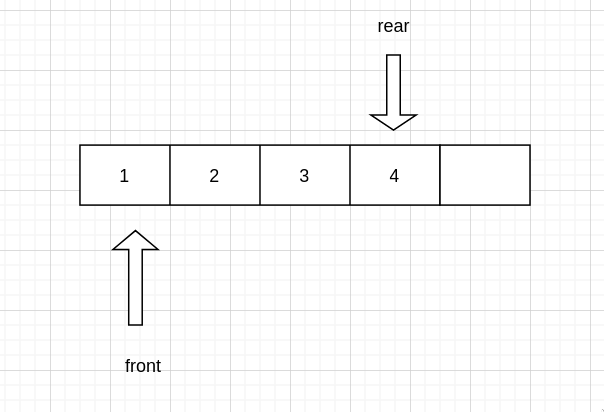
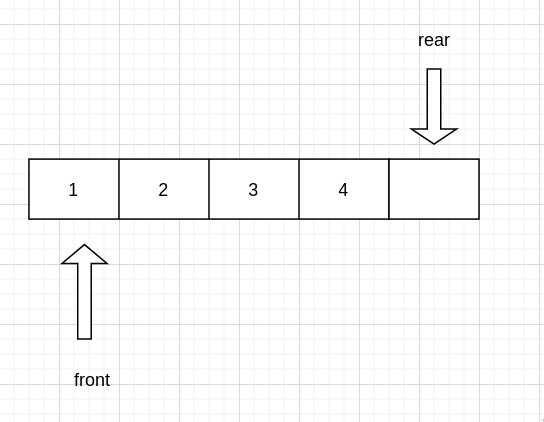
现在已经入了 4 个值，再继续入队，queue->front = 0, (queue->rear + 1) % SIZE = 0, 我们发现 front == (rear+1)%SIZE 了，从位置上来说 rear 和 front 的确已经相邻，判断没有出问题，但是实际上 rear 指向的那个值并没有存东西

我们现在回想一下最初初始化 queue 的时候

我们发现 rear 指向的值也没有值，而每次入队后，rear 指向的都是 queue 实际队尾的后面那个位置

所以循环队列总会浪费一个空间。

链式存储

定义

从上面的分析可以发现，顺序存储的单端普通队列有着顺序存储的缺点，即容量固定，当队列容量不定时，链式存储能发挥它的优势。

链式存储，是由每个 node 连接而成的，所以我们先来定义 node

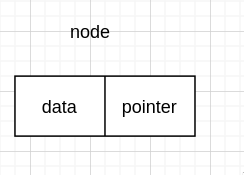
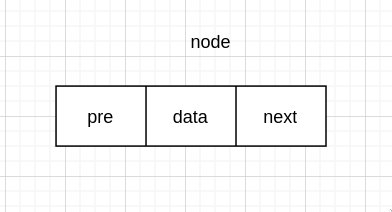
每个 node 需要存数据 data，和下一个 node 的地址。

// 队伍每个节点
typedef struct {
    int data;
    struct Node *next;
} Node;

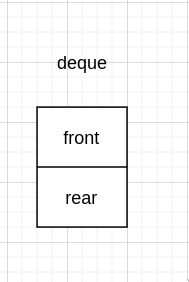
然后队列不同于普通的单链表，除了在元素的增删上有区别外，链式存储的队列还需要存两个地址，即 front 和 rear，而单链表只需要存首地址 head 即可。

// queue
typedef struct {
    Node *front;
    Node *rear;
} Queue;

如同单链表可以增加一个首节点，链队列也可以选择增加首节点。

有头节点

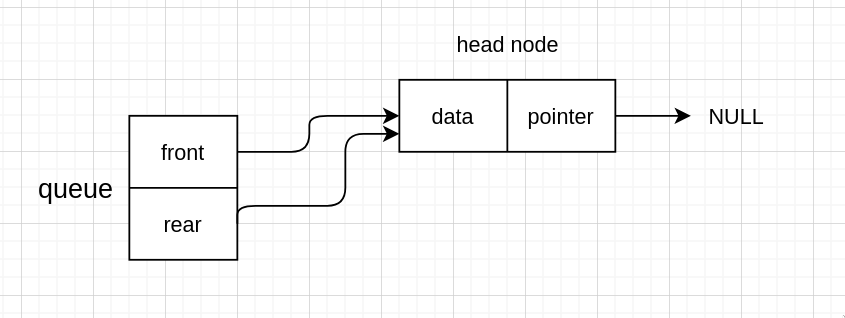
无头节点

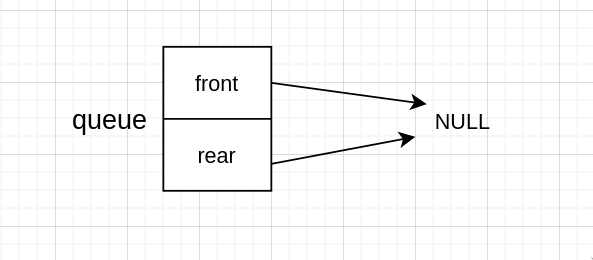
单端队列出队都是在 rear 处，有没有头节点对于出队而言没有什么影响。

但是对于入队来说，没有头节点需要同时修改 front 和 rear，而有头节点直接修改 front 即可，除此外，初始化 queue，遍历 queue 都有一些区别。

初始化

如果没有头节点的话，直接给两指针分配空间

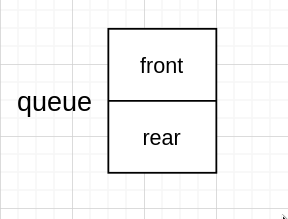
然后都指向 NULL 即可

// init queue
Queue CreateQueue() {
    // 分配给 Queue 存两个指针的内存
    Queue *queue = (Queue *) malloc(sizeof(Queue));
    // 两指针指向 NULL
    queue->rear = NULL;
    queue->front = NULL;

    return *queue;
}

而如果有头节点的话，则除了需要给指针分配空间，还要分配一个新节点

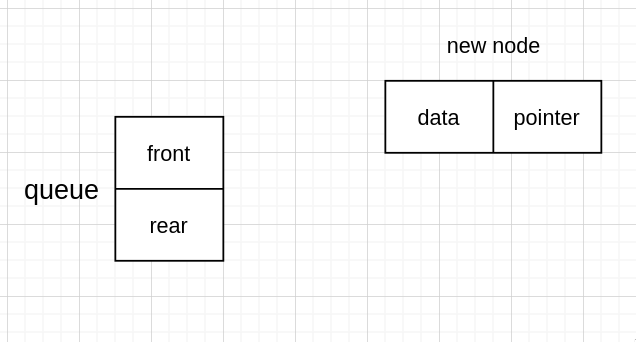
然后新节点指向 NULL

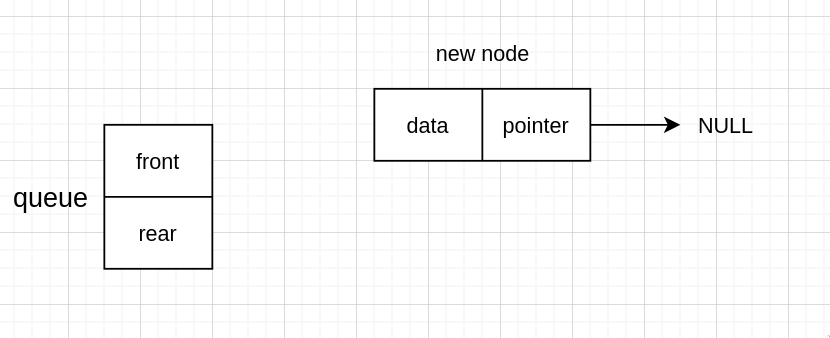
再指针指向这个节点

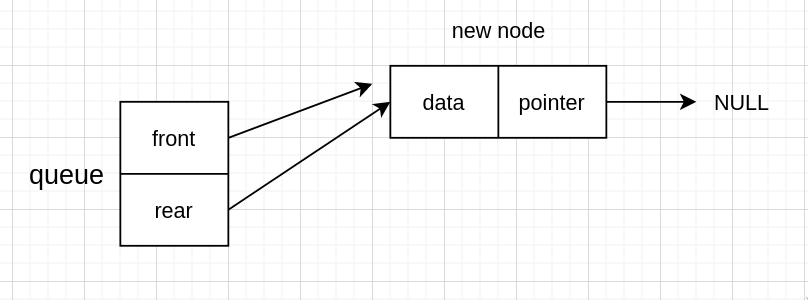
// 初始化队伍
Queue CreateQueue() {
    // 分配给 Queue 存两个指针的内存
    Queue *queue = (Queue *) malloc(sizeof(Queue));
    // 分配首节点
    Node *new_node = (Node *) malloc(sizeof(Node));
    // 首节点下一个指向 NULL
    new_node->next = NULL;
    // queue 两指针指向首节点
    queue->front = new_node;
    queue->rear = new_node;

    return *queue;
}

入队

如果有头节点，需要先新建一个 node

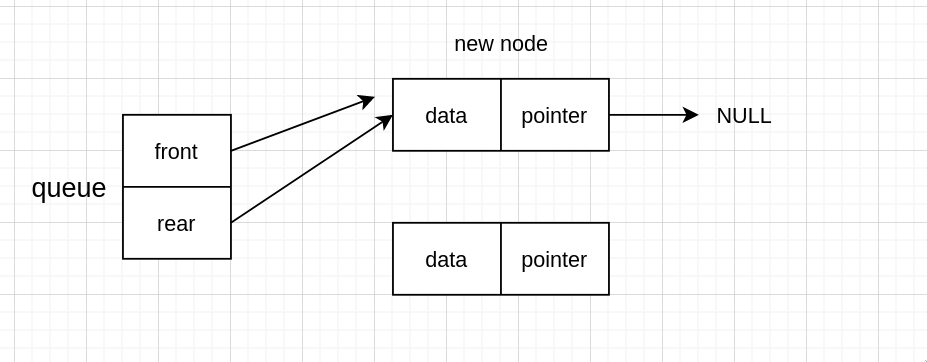
存值

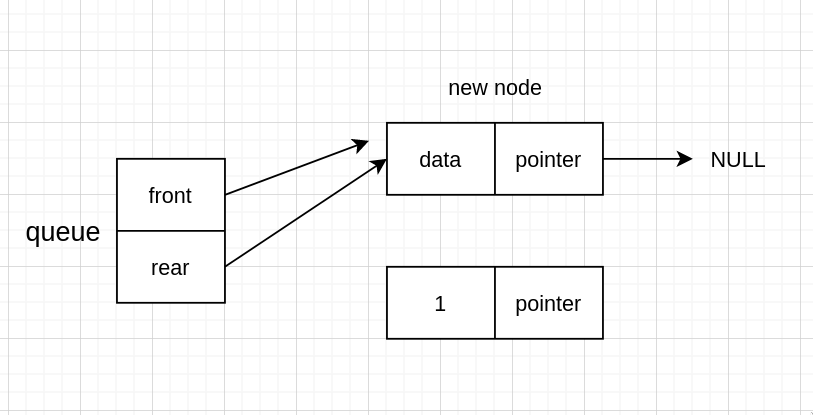
新 node 指向 NULL，因为新 node 会变成队尾，而队尾是指向 NULL 的

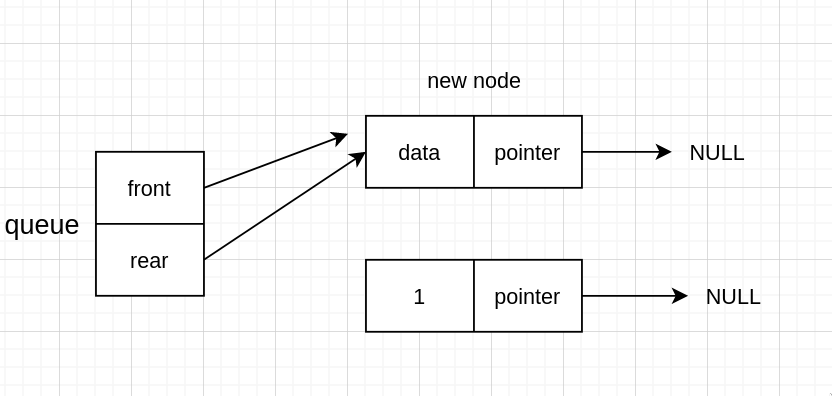
然后尾节点指向新节点

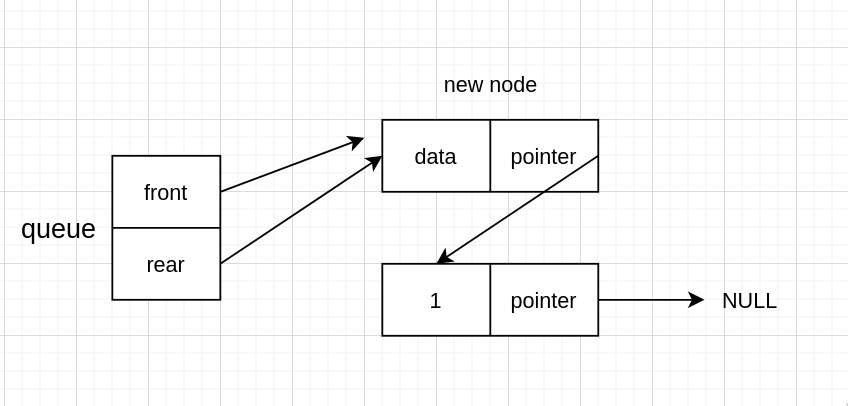
再尾指针指向新节点，即新的尾节点

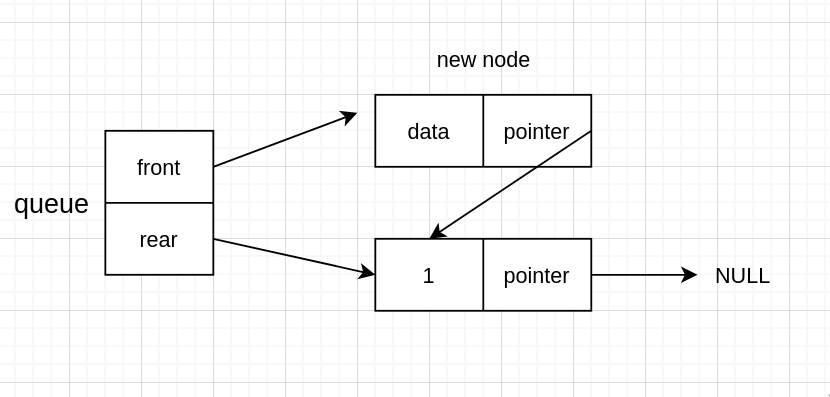
换为代码

// 入队
void EnQueue(Queue *queue, int data) {
    // 建立新 node
    Node *new_node = (Node *) malloc(sizeof(Node));
    // 存值
    new_node->data = data;
    // 新 node 对成为队尾，队尾指向 NULL
    new_node->next = NULL;
    // 尾节点连接新 node
    queue->rear->next = (struct Node *) new_node;
    // 尾指针指向新 node
    queue->rear = new_node;
}

这是有首节点的入队方式，如果没有首节点的话，第一次入队有些不同

这是初始化后的样子

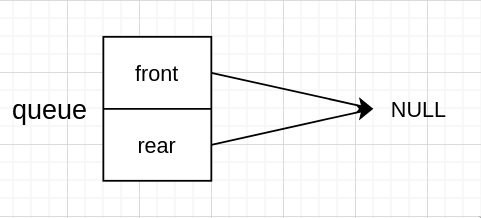
然后判断 queue 是第一次入队后，即判断 front 和 rear 都等于 NULL 后

新建 node

新 node 存值

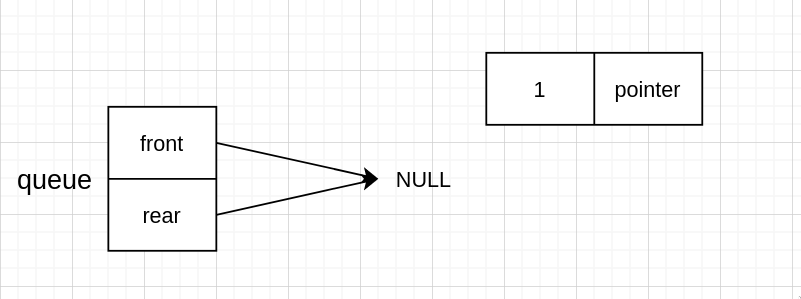
新 node 连接 NULL

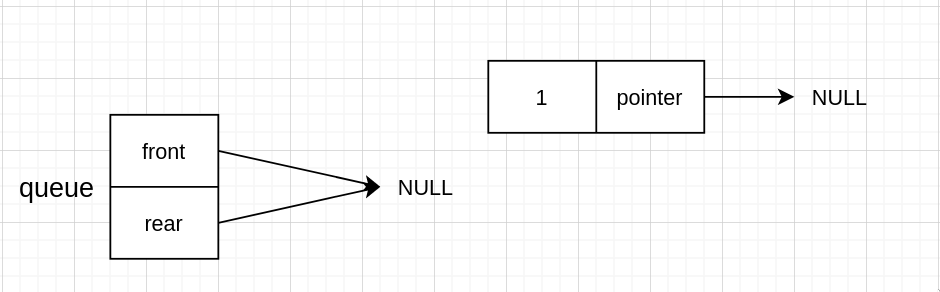
然后两指针都指向新 node

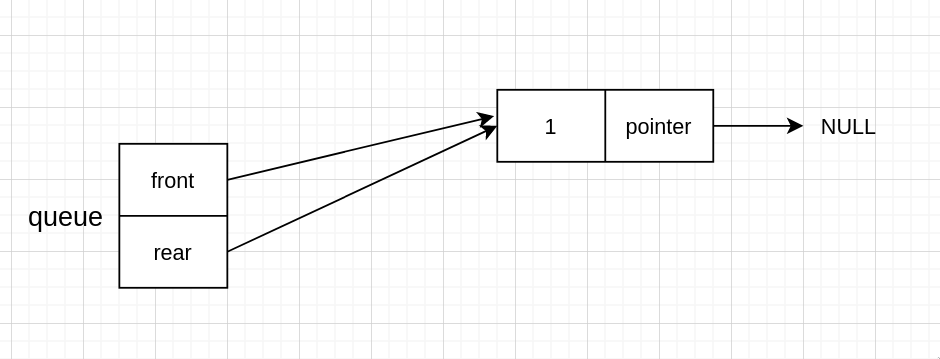
这之后就和普通的入队方式没有什么区别了

代码

// 入队
void EnQueue(Queue *queue, int data) {
    // 建立新 node
    Node *new_node = (Node *) malloc(sizeof(Node));
    // 存值
    new_node->data = data;
    // 新 node 对成为队尾，队尾指向 NULL
    new_node->next = NULL;

    // 如果是没有头节点，且第一次入队
    if (queue->rear == NULL && queue->front == NULL) {
        queue->rear = new_node;
        queue->front = new_node;
        return;
    }

    // 尾节点连接新 node
    queue->rear->next = (struct Node *) new_node;
    // 尾指针指向新 node
    queue->rear = new_node;
}

出队

入队时没有容量限制，但是出队要注意是否为空队，所以我们都需要先判断一下是否为空队。

而无论是有头节点

还是没有头节点

都只需判断 front 是否等于 rear 即可。

我们继续来先看有头节点的出队

现在假设队伍是这样的

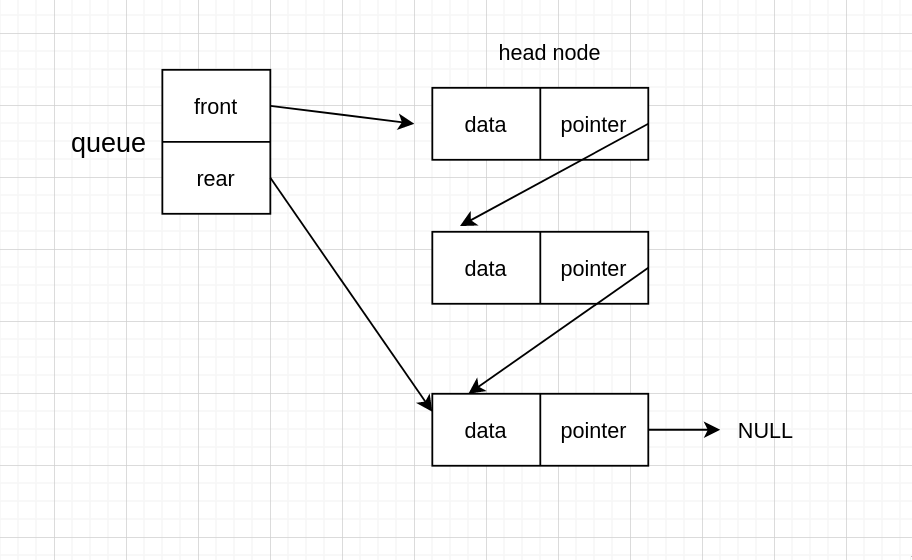
出队是出队首，但是有头节点的话，应该是头节点下一个节点，即这个

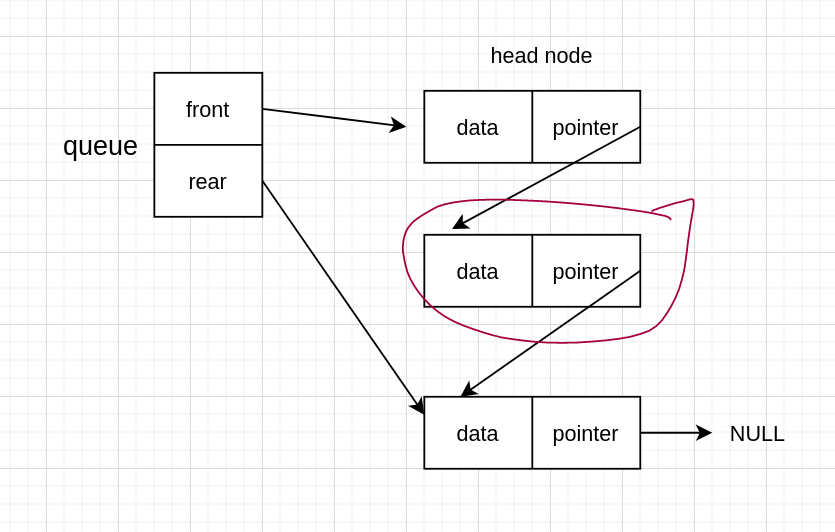
因为是链式存储，我们需要自己释放内存，所以先备份要出的那个节点

建立一个指针，然后指向这个节点

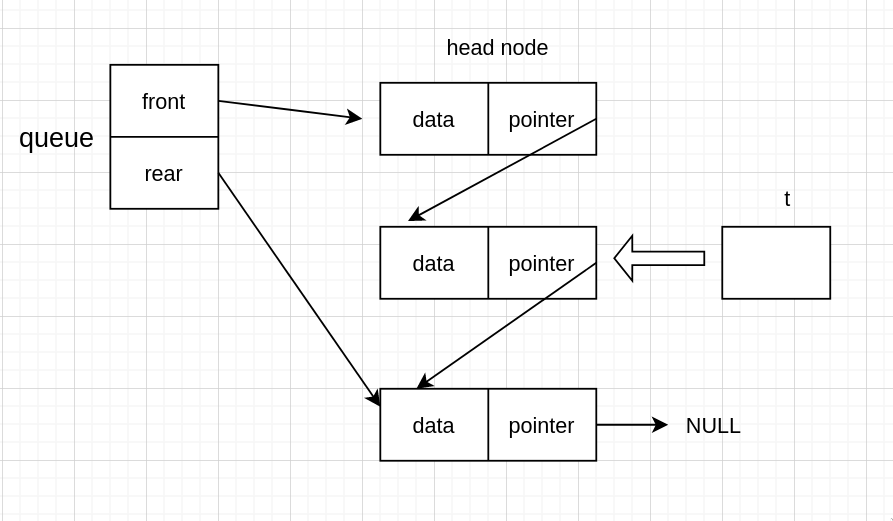
然后头节点指向队首节点的下一个

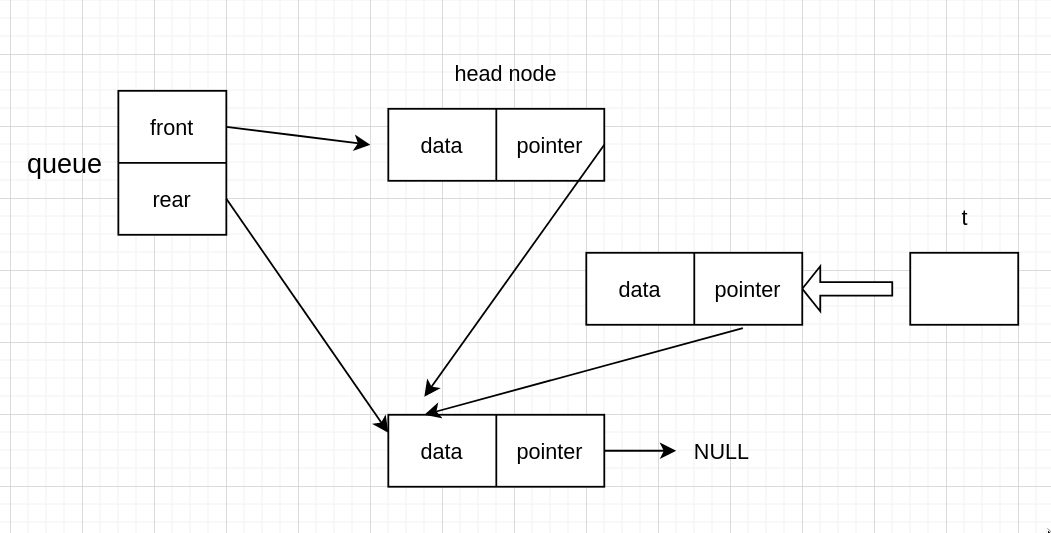
然后释放备份的节点

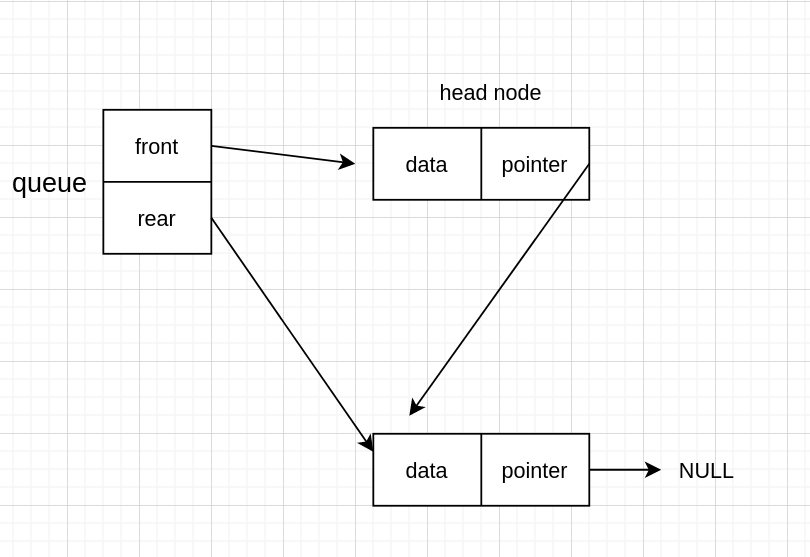
代码

// 出队
void DeQueue(Queue *queue) {
    // 判断是否为空队
    if (queue->front == queue->rear) {
        return;
    }
    // 备份队首
    Node *t = queue->front->next;
    // 出队
    queue->front->next = t->next;
    // 释放队首内存
    free(t);
}

而对于没有头节点的队列来说，需要删除的则是这个

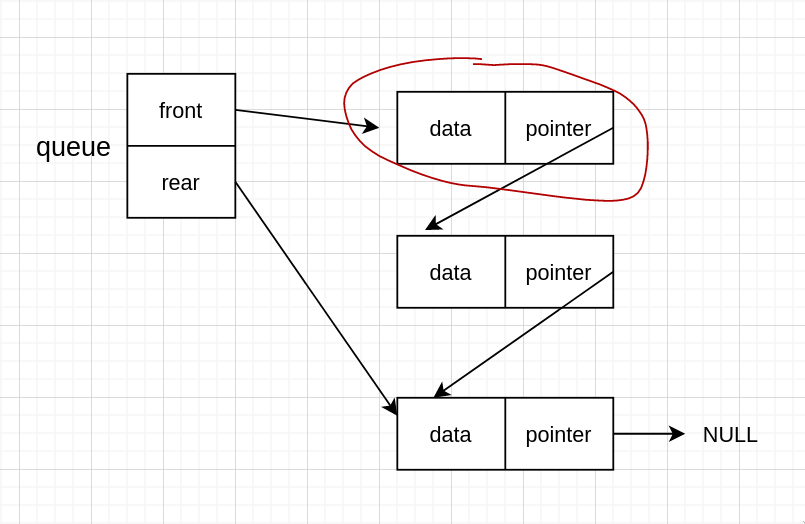
类似的，先备份

出队

然后释放内存，主要出队时和有头节点的区别

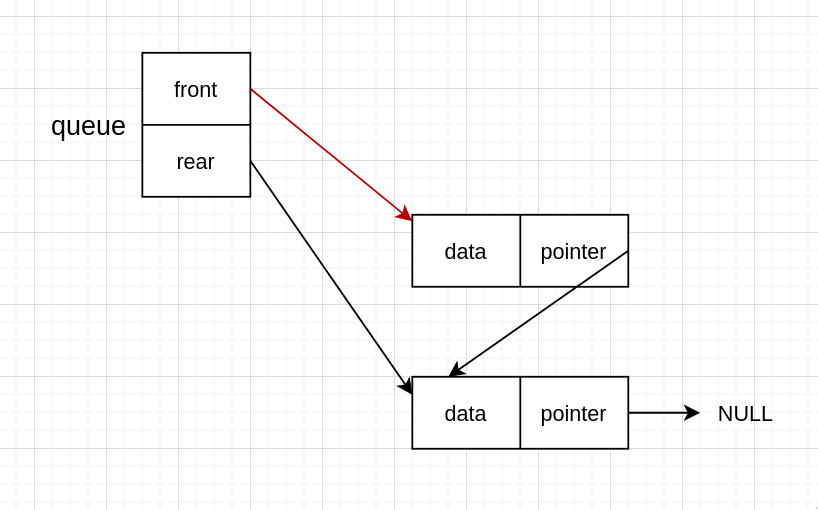
不过这里需要注意一下，当只有一个节点，而又出队时

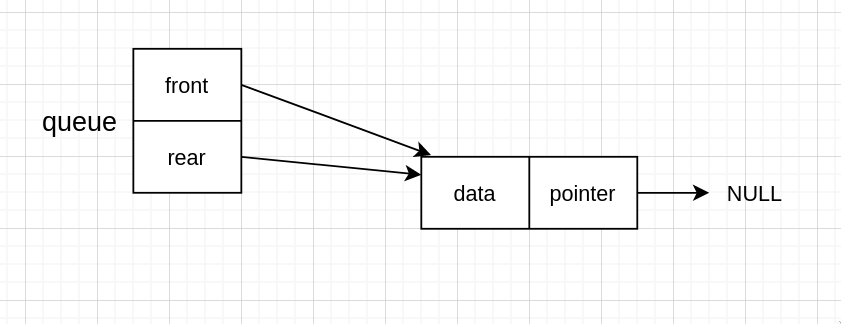
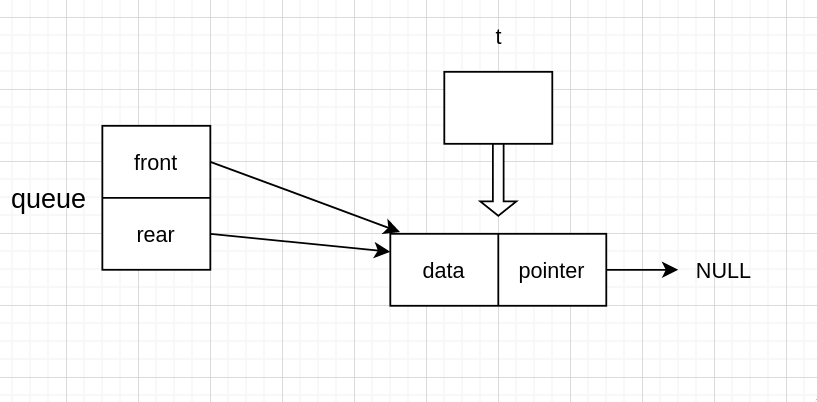
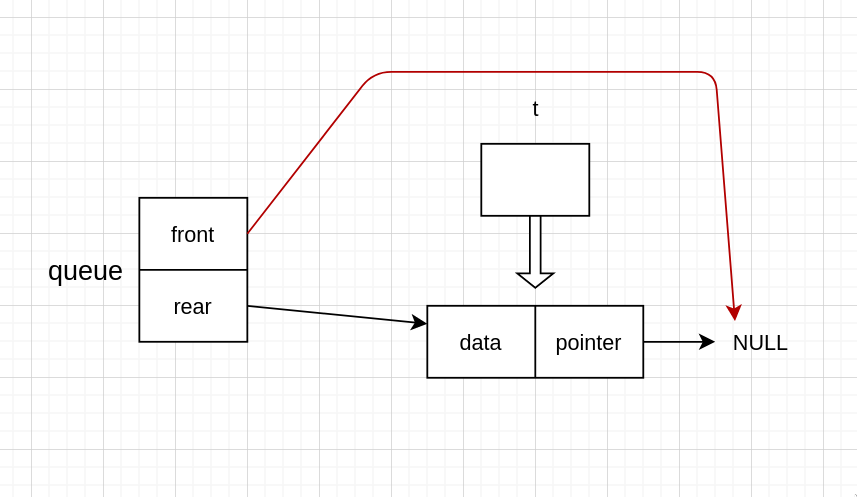
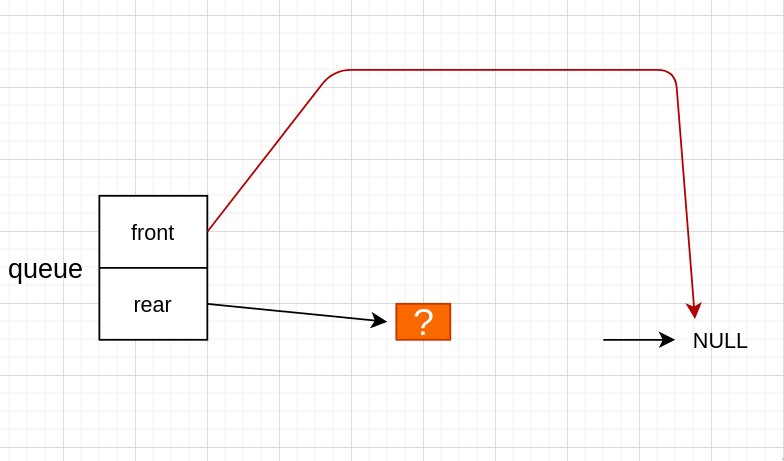
当出队后，rear 仍然指向上一个 node 的地址，但是那个 node 已经被释放了，所以需要把它改为指向 NULL 才行

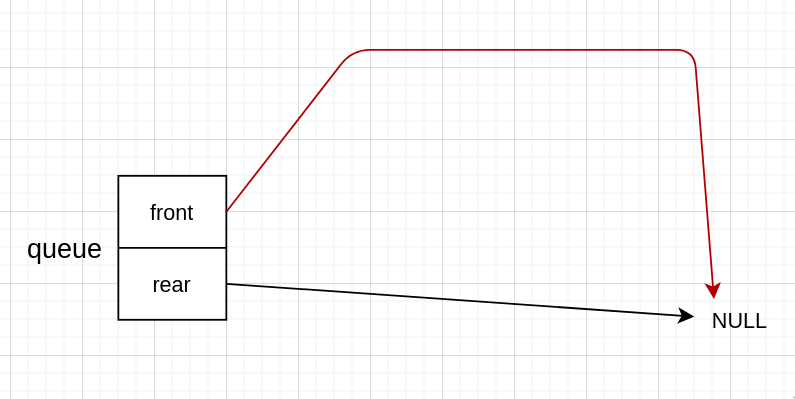
换为代码

// 出队
void DeQueue(Queue *queue) {
    // 判断是否为空队
    if (queue->front == queue->rear) {
        return;
    }
    // 备份队首
    Node *t = queue->front;
    // 出队
    queue->front = t->next;
    // 释放队首内存
    free(t);
    // 判断是否又变为空 queue
    if (queue->front == NULL) {
        queue->rear = NULL;
    }
}

实际操作

无头节点

#include <stdio.h>
#include <stdlib.h>

// 队伍每个节点
typedef struct {
    int data;
    struct Node *next;
} Node;

// queue
typedef struct {
    Node *front;
    Node *rear;
} Queue;

// init queue
Queue CreateQueue() {
    // 分配给 Queue 存两个指针的内存
    Queue *queue = (Queue *) malloc(sizeof(Queue));
    // 两指针指向 NULL
    queue->rear = NULL;
    queue->front = NULL;

    return *queue;
}

// 入队
void EnQueue(Queue *queue, int data) {
    // 建立新 node
    Node *new_node = (Node *) malloc(sizeof(Node));
    // 存值
    new_node->data = data;
    // 新 node 对成为队尾，队尾指向 NULL
    new_node->next = NULL;

    // 如果是没有头节点，且第一次入队
    if (queue->rear == NULL && queue->front == NULL) {
        queue->rear = new_node;
        queue->front = new_node;
        return;
    }

    // 尾节点连接新 node
    queue->rear->next = (struct Node *) new_node;
    // 尾指针指向新 node
    queue->rear = new_node;
}

// 出队
void DeQueue(Queue *queue) {
    // 判断是否为空队
    if (queue->front == queue->rear) {
        return;
    }
    // 备份队首
    Node *t = queue->front;
    // 出队
    queue->front = t->next;
    // 释放队首内存
    free(t);
    // 判断是否又变为空 queue
    if (queue->front == NULL) {
        queue->rear = NULL;
    }
}

void TraverseQueue(Queue queue) {
    while (queue.rear != queue.front) {
        printf("%d\n", queue.front->data);
        queue.front = queue.front->next;
    }
    printf("%d\n", queue.front->data);
};


int main(void) {
    Queue queue = CreateQueue();
    EnQueue(&queue, 1);
    EnQueue(&queue, 2);
    EnQueue(&queue, 3);
    EnQueue(&queue, 4);
    EnQueue(&queue, 5);

    TraverseQueue(queue);

    printf("###\n");

    DeQueue(&queue);
    DeQueue(&queue);
    TraverseQueue(queue);

    return 0;
}

有头节点

#include <stdio.h>
#include <stdlib.h>

// 队伍每个节点
typedef struct {
    int data;
    struct Node *next;
} Node;

typedef struct {
    Node *front;
    Node *rear;
} Queue;

// 初始化队伍
Queue CreateQueue() {
    // 分配给 Queue 存两个指针的内存
    Queue *queue = (Queue *) malloc(sizeof(Queue));
    // 分配首节点
    Node *new_node = (Node *) malloc(sizeof(Node));
    // 首节点下一个指向 NULL
    new_node->next = NULL;
    // queue 两指针指向首节点
    queue->front = new_node;
    queue->rear = new_node;

    return *queue;
}

// 入队
void EnQueue(Queue *queue, int data) {
    // 建立新 node
    Node *new_node = (Node *) malloc(sizeof(Node));
    // 存值
    new_node->data = data;
    // 新 node 对成为队尾，队尾指向 NULL
    new_node->next = NULL;
    // 尾节点连接新 node
    queue->rear->next = (struct Node *) new_node;
    // 尾指针指向新 node
    queue->rear = new_node;
}

// 出队
void DeQueue(Queue *queue) {
    // 判断是否为空队
    if (queue->front == queue->rear) {
        return;
    }
    // 备份队首
    Node *t = queue->front->next;
    // 出队
    queue->front->next = t->next;
    // 释放队首内存
    free(t);
}

void TraverseQueue(Queue queue) {
    queue.front = queue.front->next;
    while (queue.rear != queue.front) {
        printf("%d\n", queue.front->data);
        queue.front = queue.front->next;
    }
    printf("%d\n", queue.front->data);
};


int main(void) {
    Queue queue = CreateQueue();
    EnQueue(&queue, 1);
    EnQueue(&queue, 2);
    EnQueue(&queue, 3);
    EnQueue(&queue, 4);
    EnQueue(&queue, 5);

    TraverseQueue(queue);

    printf("###\n");

    DeQueue(&queue);
    DeQueue(&queue);
    DeQueue(&queue);
    TraverseQueue(queue);


    return 0;
}

双端队列

双端队列即在队首，队尾都支持入队出队的队列，同样的可以顺序存储，或链式存储。不过顺序存储的话，如果是刚开始在 array[0] 处，无论是队首还是队尾都不能完全支持入队或出队，除非是在 array 中间某处开始。

或者用 array 来实现环状的双端队列的话，也能实现，不过考虑的情况就有些多了，这里还是拿链式存储来做例子。

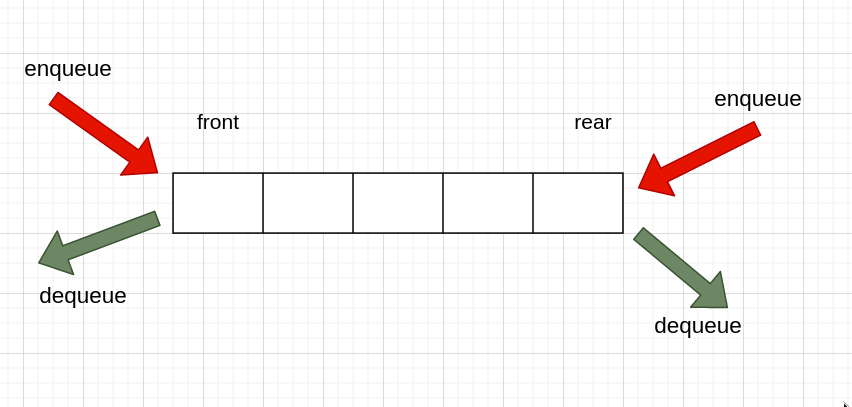
定义

typedef struct {
    int data;
    struct Node *next;
    struct Node *pre;
} Node;

typedef struct {
    Node *front;
    Node *rear;
} Deque;

初始化

同样的，链式存储的双端队列也有头尾节点或没有头尾节点的情况。

没有头，尾节点

Deque CreateDeque() {
    Deque *deque = (Deque *) malloc(sizeof(Deque));
    deque->rear = NULL;
    deque->front = NULL;

    return *deque;
}

有头，尾节点

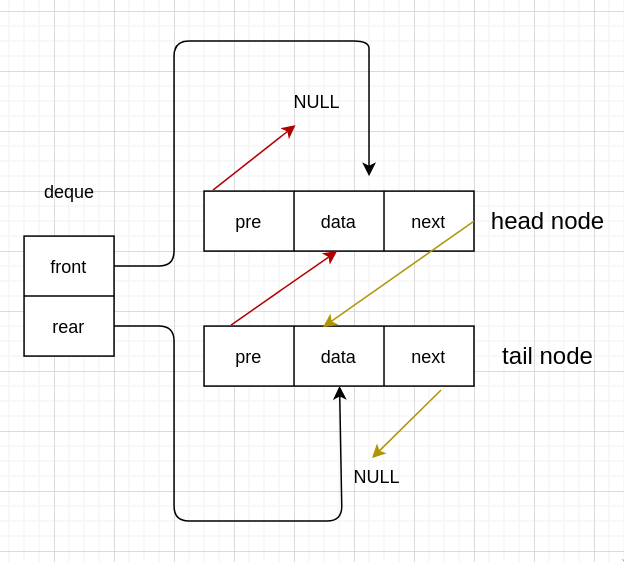
Deque CreateDeque() {
    Deque *deque = (Deque *) malloc(sizeof(Deque));

    Node *head_node = (Node *) malloc(sizeof(Node));
    Node *tail_node = (Node *) malloc(sizeof(Node));

    head_node->pre = NULL;
    head_node->next = tail_node;
    tail_node->next = NULL;
    tail_node->pre = head_node;

    deque->front = head_node;
    deque->rear = tail_node;

    return *deque;
}

队列主要的操作就是入队和出队，而双端队列则有四种情况。

队首入队

有头节点

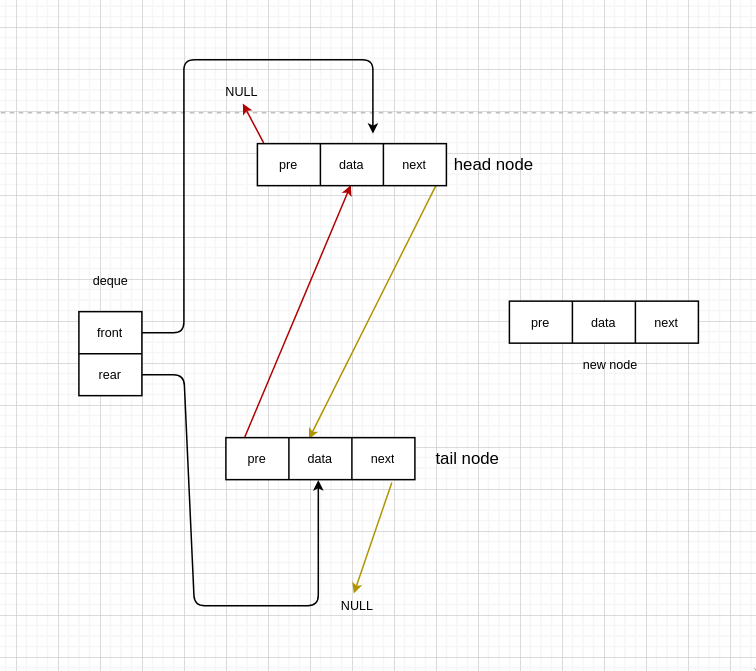
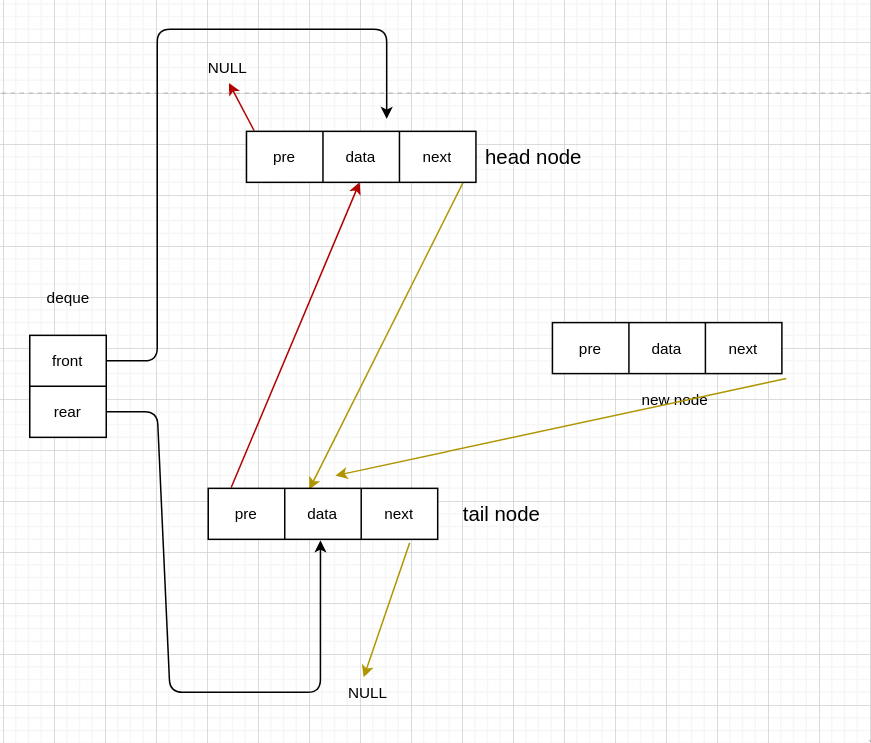
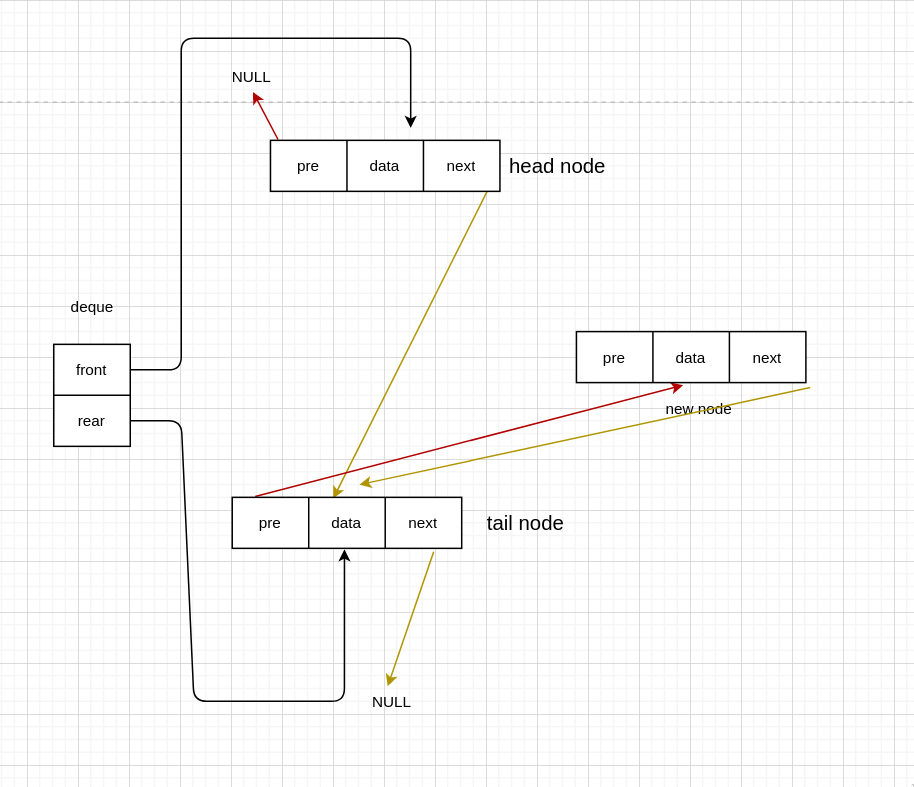
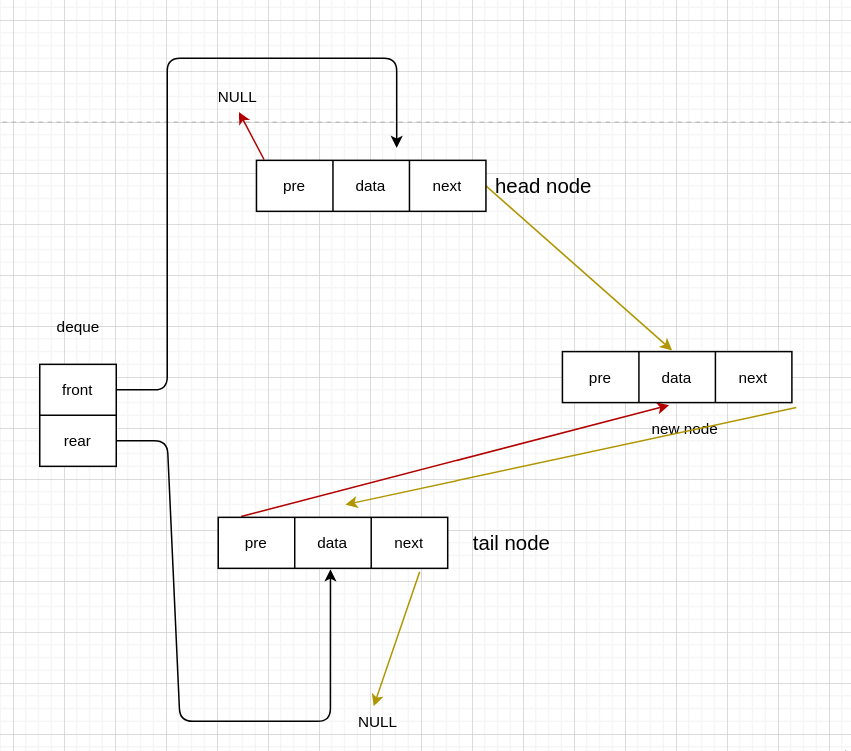
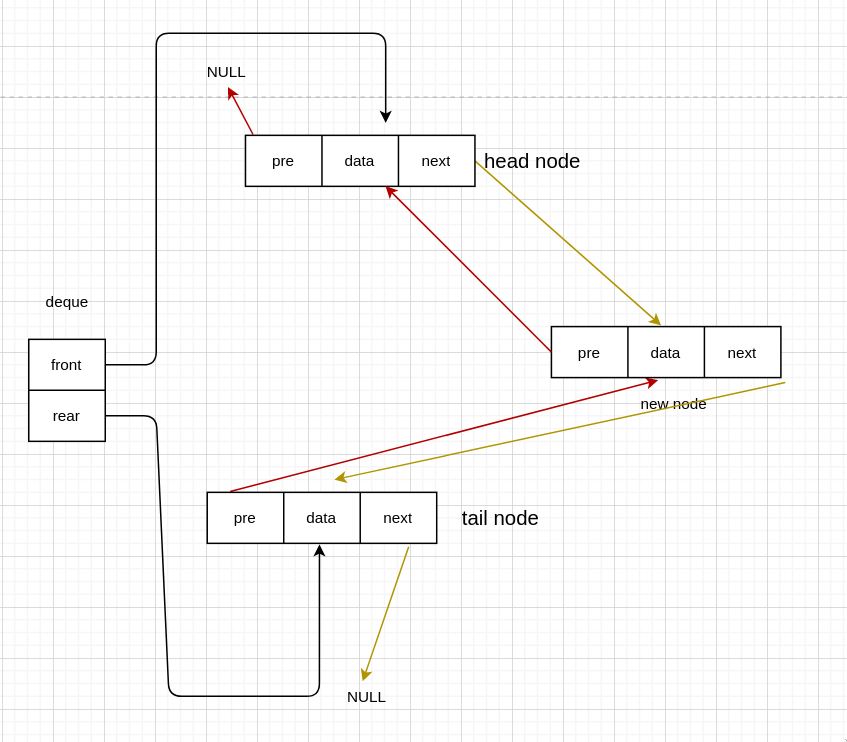
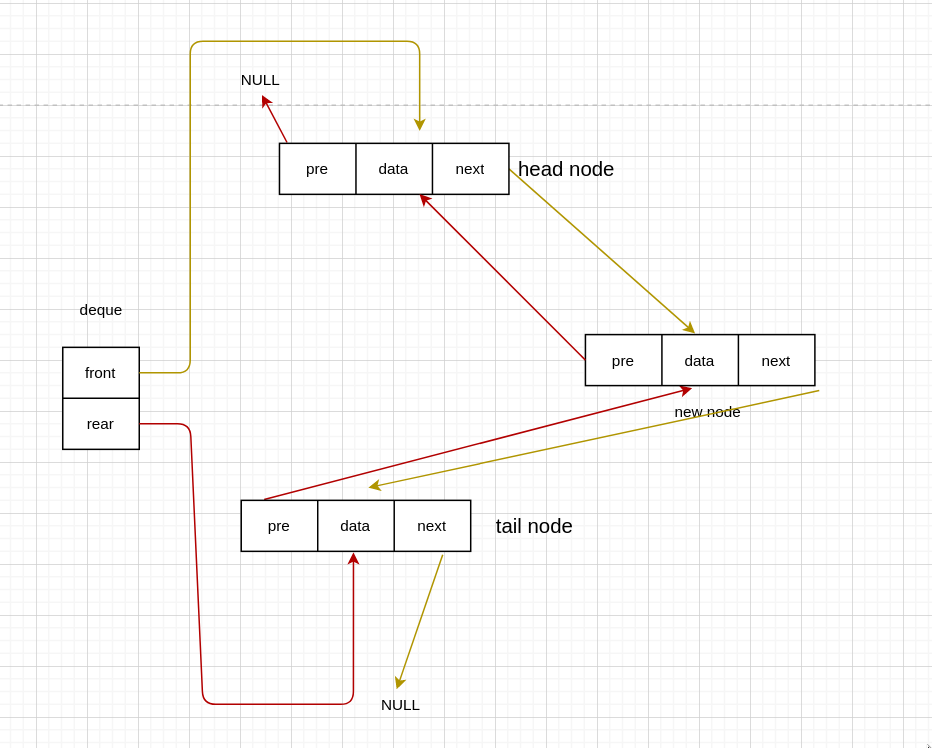
void InsertFront(Deque *deque, int data) {
    Node *new_node = (Node *) malloc(sizeof(Node));
    new_node->data = data;
    new_node->next = deque->front->next;
    Node *t = deque->front->next;
    t->pre = new_node;
    deque->front->next = new_node;
    new_node->pre = deque->front;
}

没有头节点

第一次入队

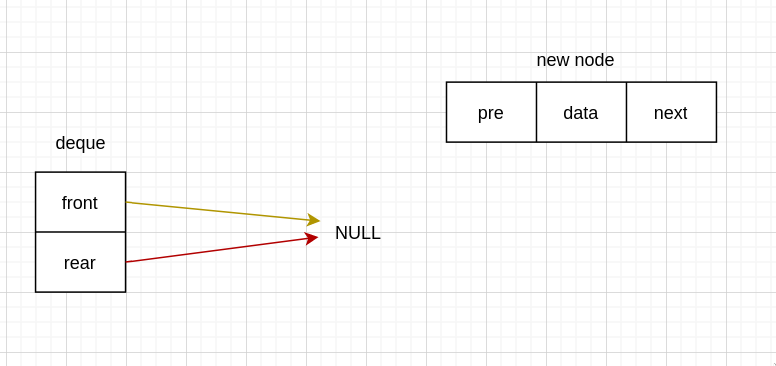
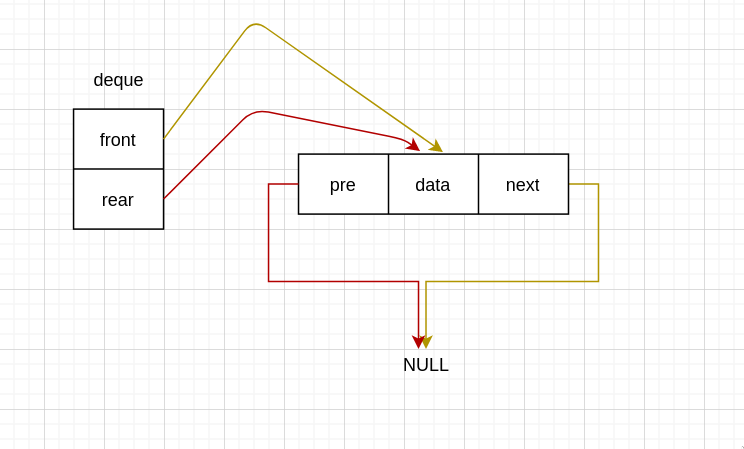
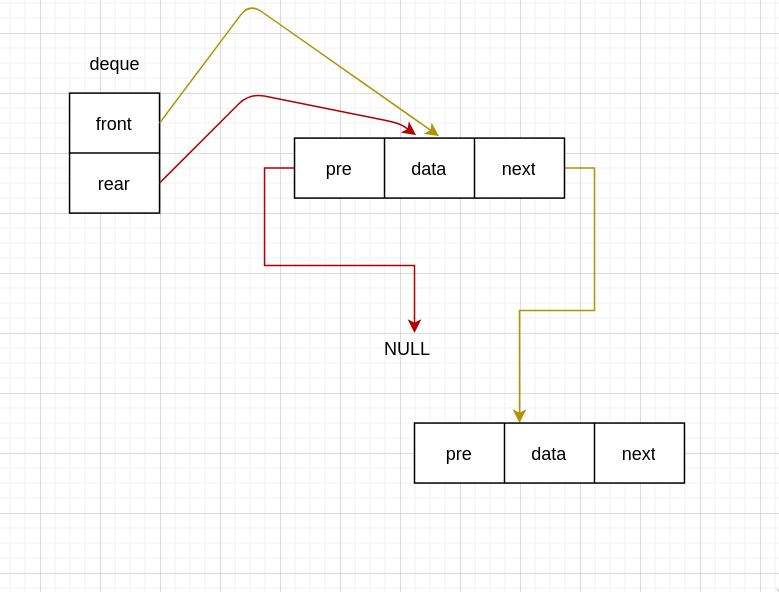
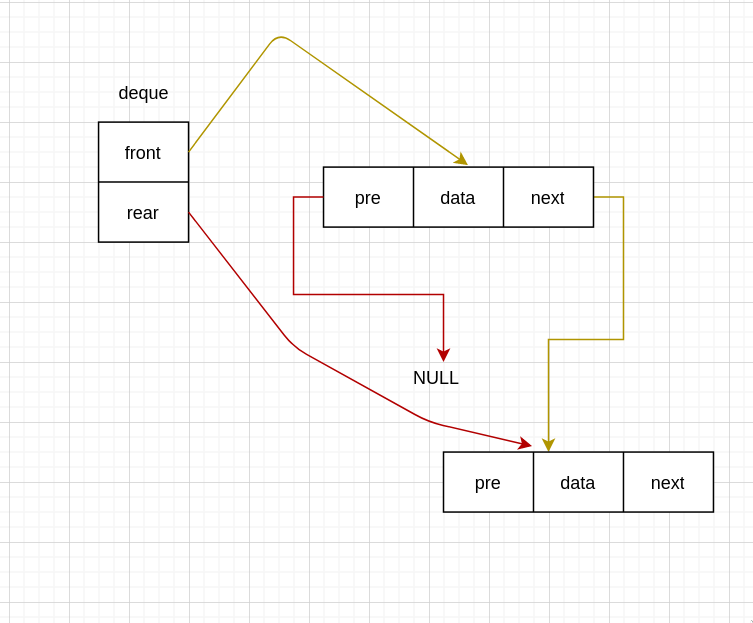
void InsertFront(Deque *deque, int data) {
    Node *new_node = (Node *) malloc(sizeof(Node));
    new_node->data = data;

    // 第一次入队
    if (deque->front == NULL && deque->rear == NULL) {
        new_node->pre = NULL;
        new_node->next = NULL;
        deque->rear = new_node;
        deque->front = new_node;
        return;
    }
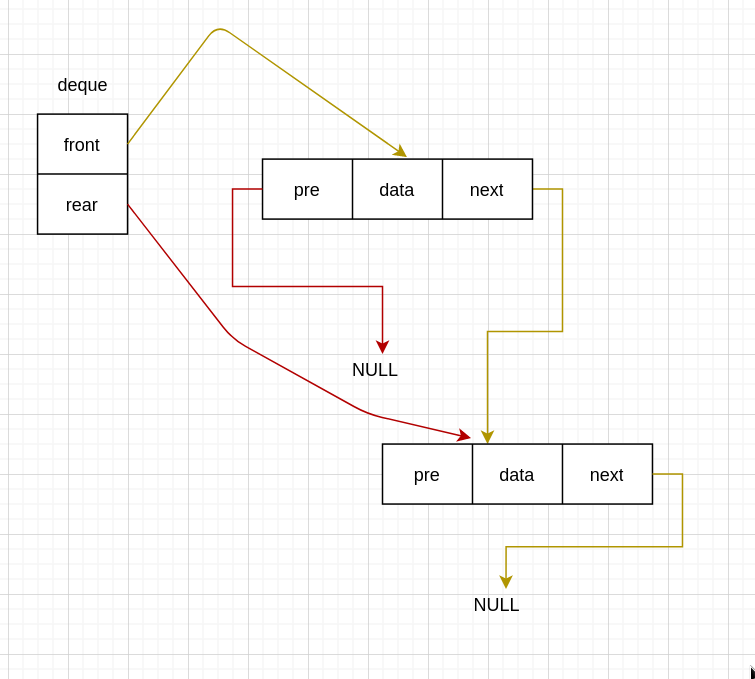
    // 第二次入队
    if (deque->front->next == NULL && deque->rear->pre == NULL) {
        deque->front->next = new_node;
        deque->rear = new_node;
        new_node->next = NULL;
        new_node->pre = deque->front;
        return;
    }
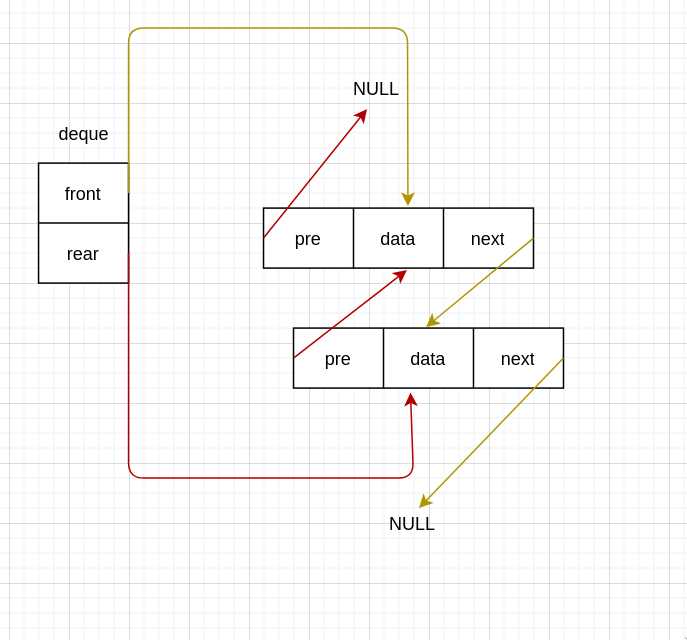
    new_node->next = deque->front->next;
    Node *t = deque->front->next;
    t->pre = new_node;
    deque->front->next = new_node;
    new_node->pre = deque->front;
}

队首出队

队尾入队

队尾出队

优先队列

参考

数据结构之 循环队列 顺序队列 C 语言数据结构之链队列

链式队列及基本操作（C 语言）完全攻略

队列

大话数据结构第4章

数据结构与算法 07—— 链队列