图解链表

前言

这篇文章是我学习链表的笔记总结，没有主要参考的书籍，尝试过阅读《大话数据结构》，但是这本书读着不太舒服，主要参考各种博客，以及刷了一些 leetcode 上的链表的题来巩固。

这篇文章同样的，在使用一些术语时，我会尽量使用英文。另外有大量的原创图，以及 c 语言的具体实现。

链表

介绍

链表(linked list) 是一种线性表（linear list），元素（element）间一对一，逻辑上相连，但是在内存上分配不连续。

链表每个元素被称为节点（node), 由数据域（data filed）和 指针域（pointer filed) 组成。

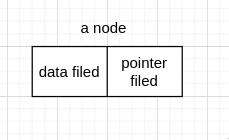
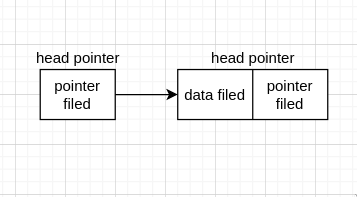
linked list 的每个 node 在内存上并不相连，如

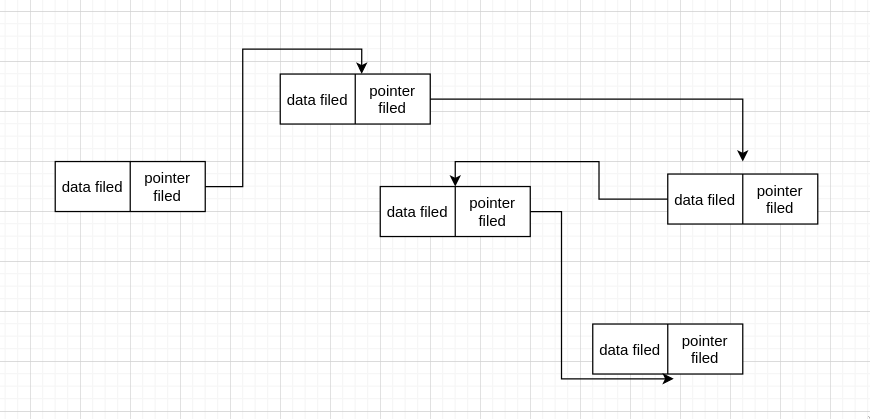
因此，node 间想要相连，就需要知道下一个 node 的 address，这就要借助 pointer。故每个 node 的 data filed 存这个 node 的 data， 而 pointer filed 则存下一个 node 的 address。

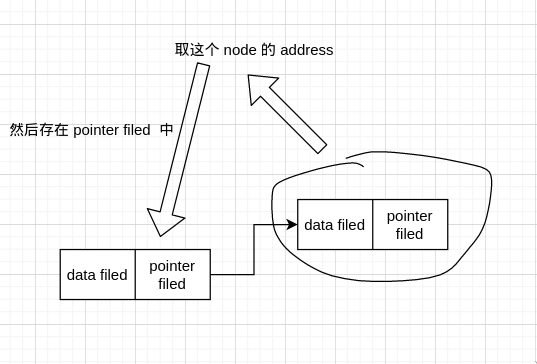
我们知道链表的节点是有限的，所以最后一个 node 就没有下一个 node，故最后一个 node 的 pointer filed 存的 addres 就为 NULL.

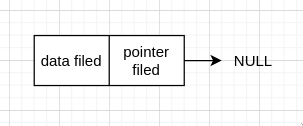
性质

因为每个 node 都存下一个node 的 address，所以要访问一个 node 的话，就需要知道上一个 node 才行，故 linked list 查找（search） 元素，更新（update）元素，插入元素（insert），删除（delete）元素都需要先找到这个 node，所以就需要遍历链表。

search 和 update 需要遍历链表，故需要一个一个的找，时间复杂度是 O(n).

insert 和 delete 不算遍历的过程，只是执行 insert 和 delete 的话，只需更改 address 即可，故时间复杂度是 O(1).

这里看字不容易理解，可以继续往下看具体的代码实现，那里有详细的图解说明。

头指针/头节点/首元节点

这三个是链表中容易搞混的概念，我们这里用来解释一下。

我们现在知道链表是由 node 组成的，现在我们先来弄几个 node 组成的链表

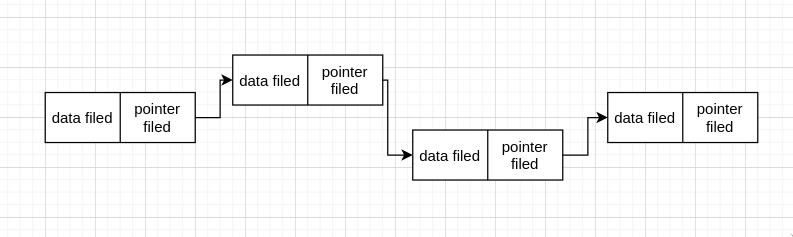
现在我们要操作这个链表，肯定需要知道首地址(head address)，如果我们要在函数中操作这个链表，也需要把首地址传进去，那干脆直接用个头指针(head pointer) 指向第一个节点，这个指针就是 head pointer, 我们需要操作链表，所以这个是必须要有的

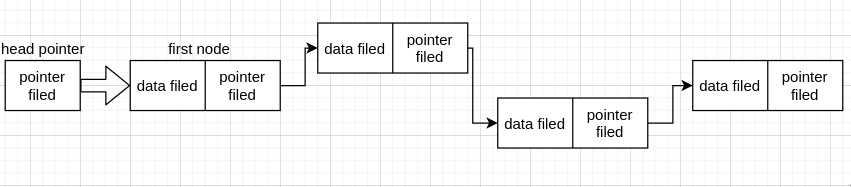
现在如果我们要在链表中间插入 node, 前面有 node，操作方式都是一样的，但是如果我们要在第一个节点前加一个 node 的话，前面没有 node， 那么在 intert 函数中肯定要分情况。

同样的，由有链表在内存中是不连续分配的，那么我们怎么知道一共有多少个 node 呢，所以为了解决这些问题，有时候我们会在第一个节点前，也就是存真正的数据前的那个节点前再加一个节点，这个节点的 data filed 用来存链表长度等特殊的信息。同时操作插入第一个节点也比较方便，这个节点就叫头节点 (head node)

现在我们已经知道头节点和头指针是怎么回事了，首元节点就比较容易理解了，也就是存正式数据的第一个节点，如上面的 first node, 这是为了区分头节点取的名字

因为有 head node 和没有 head node 这两种情况，所以在一些操作上也是有差距的，具体要看实际情况。

如没有 head node 的空表, 直接头指针连接 NULL

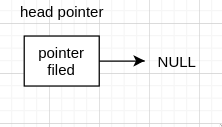
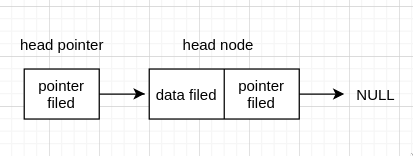
而有 head node 的空表，则是 head node 连接 NULL

分类

链表在逻辑上都是一对一的关系，一般我们说的都是动态链表，即在物理上元素间靠指针相连，个数不定。

而在声明链表时就划分好一定的内存（相连的），靠 array 的形式组成的链表，被称为静态链表。

一般不主动说明是静态链表时，都说的是动态链表。

注意静态链表和顺序表的区别。

单链表(single linked list node)：每个节点只存下一个节点的地址和数据

单链表的节点

普通的单链表

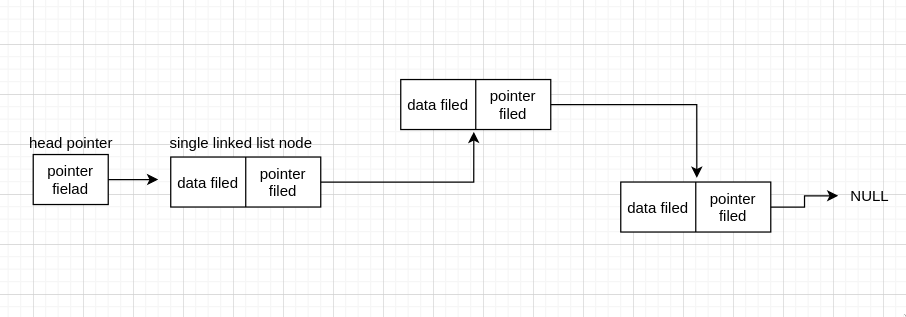
单链表中还有一种特殊的情况，尾节点（tail node）不指向 NULL，而指向 head pointer，那这个链表就成为了一个环，这个链表叫做单向循环链表（circular linked list）

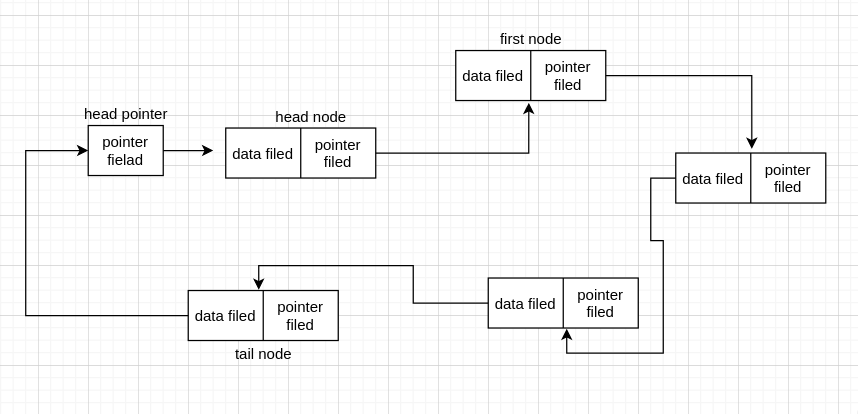
双链表（double linked list）对应于单链表，双链表每个 node 存上一个和下一个 node 的地址，以及 data。

节点

双链表

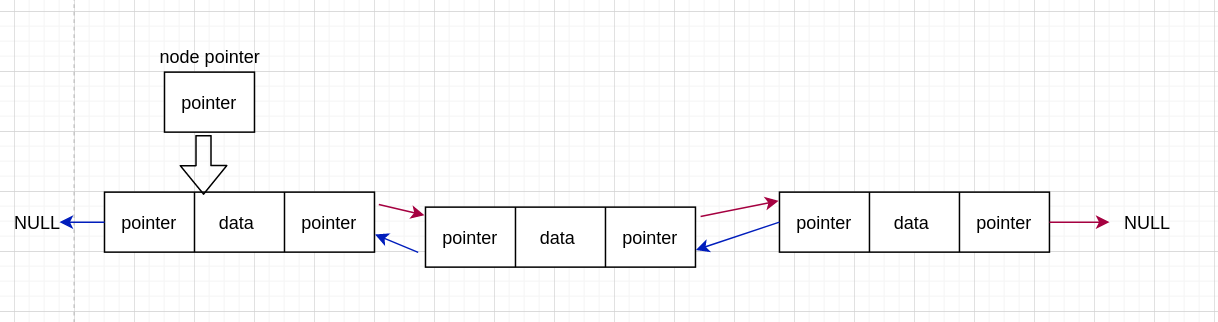
我们在上面说了单链表中有单向循环链表这种特殊情况，容易理解，双链表中也有这种情况。双链表的尾节点（tail node） 指向 head node，那这个链表即双向循环链表。

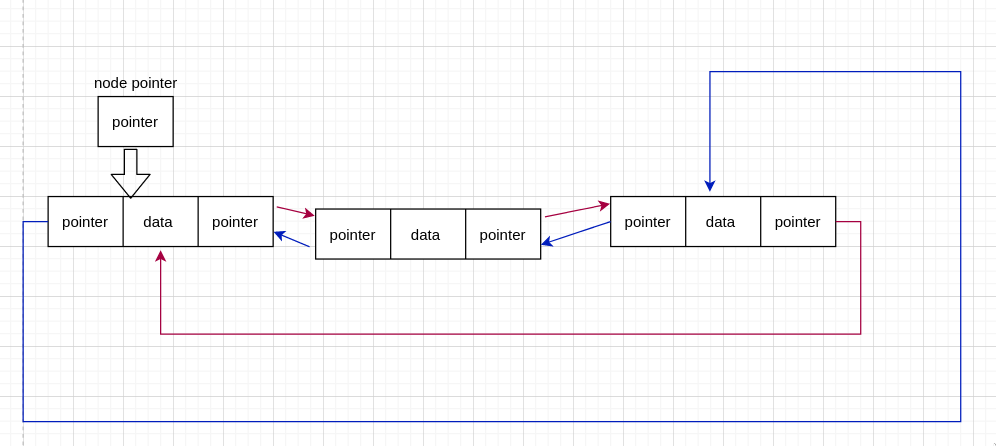
单链表

create

单链表是链表中的一种，每个 node 存下一个 node 的地址以及数据，单链表是单向的。

single linked list 是由 node 组成的，要实现的话首先就要实现 node

// single linked list node
typedef struct {
    int data;  // data filed
    struct Node *next;  // pointer filed
} Node;

这段代码声明了 single linked list 的 node ，然后声明了存数据的 data，以及存下一个 node address 的 next.

我们在前面说了，单链表可以有头节点或没有，很多时候我们会建立头节点，所以这里还是以有头节点为例子。

我们继续，来创个函数来声明 single linked list

// CreateList 建立一个有头节点的单链表
Node *Createlist() {
    // 头节点
    Node *new_node = malloc(sizeof(int));
    if (new_node == NULL) {
        printf("crete linked list failed!");
        exit(-1);
    }
    // 空表，指向 NULL
    new_node->next = NULL;
//    new_node->data=  0;
    return new_node;
}

这个函数建立了一个有头节点的单链表，然后返回头节点，要使用的话，需要赋值给头指针，如

int main(void) {
	Node *head = Createlist();
	
	return 0;
} 

我们在这个函数中，使用 malloc 函数分配了内存给头节点，然后判断是否分配成功，再指向 NULL，然后头节点的 data filed 自己看存什么数据，这里我们没有存有意义的数据。然后返回这个头节点。

这个函数没有传入参数，而是把头节点返回，我们也可以把头节点直接传进去，如

// 传入 Node 指针的指针，因为要在函数改变 Node 指针的值
void CreateList(Node **head) {
    // 先给头节点动态分配内存，然后把头指针指向这块内存，即指向头节点
    *head = (Node *) malloc(sizeof(int));
    if (*head == NULL) {
		printf("create single linked list failed!");
	}
    (*head)->next = NULL;
//    (*head)->data = 0;
}

这个函数同样的创建了一个有头节点的单链表，不过是把头指针当做参数传进去的。需要注意的是头指针 (head) 本身是指向节点的指针（Node *)，而要在函数中改变变量的值，需要传入其地址，故这里是传入头指针的地址，则传入就是指针的指针。然后分配内存，头指针指向头节点，设置 NULL，设置 data，这和刚才返回头节点的函数是相同的。

要使用的话，需要传头指针

int main(void) {
	Node *head = NULL;
	CreateList(&head);
	
	return 0;
}

insert

链表除了操作表本身，就是操作节点了。对链表节点的插入是比较常用的，这里有几种情况。

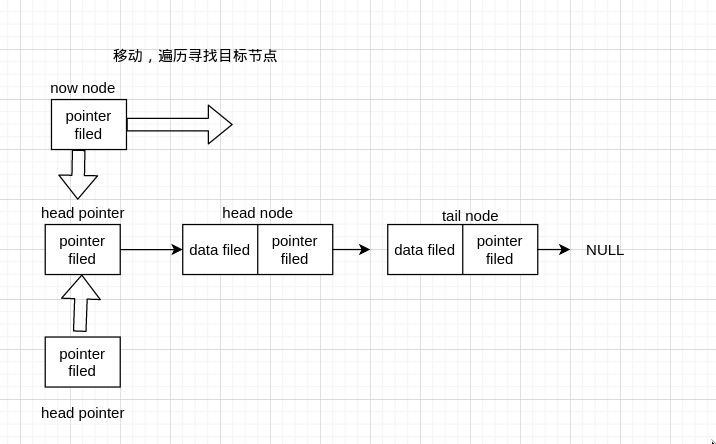
首先我们来谈谈直接在末尾插入节点，要插入节点，首先要找到目标节点的位置。链表不支持随机访问（random access), 因为每个 node 的地址是不能直接拿到的，所以只能遍历去找目标节点。

看代码

// 在单链表最后，插入一个元素， elem 是要插入的值
void InsertEndingElem(Node *head, int elem) {
    Node *now_node = head;  // 当前的 node，用于遍历 list
    Node *new_node = malloc(sizeof(int));  // 新建的 node ，即要插入的新 node

    // 判断是否新建 node 成功
    if (new_node == NULL) {
        printf("insert ending element failed!");
        exit(-1);
    }

    // 新建的 node 在 list 末尾，故需要指向 NULL， 同时设置 data
    new_node->data = elem;
    new_node->next = NULL;

    // 遍历 node，把当前 node 变为最后一个 node
    while (now_node->next != NULL) {
        now_node = now_node->next;
    }
    // 最后的 node 连接新 node
    now_node->next = new_node;
}

这个函数传入头指针和一个值，然后在末尾插入了一个新节点。

我们先建立了用于遍历的当前节点 now_head, 初始在头节点（头指针）。然后建立了新节点 now_node, 判断是否建立成功，然后把值存在新节点，又这个节点插入后就变成了尾节点，所以要指向 NULL。然后我们通过判断当前节点的下一个是否为 NULL 来判断是否到了尾节点，当前节点一直移动到尾节点。然后当前节点（指向尾节点）连接新节点，这样就插入成功了。

我们这只是插入了一个节点，也可以封装一下，插入多个节点

// 在单链表后插入多个元素， num 是数组首地址， n 是数组个数
void InsertEndingElmes(Node *head, int *nums, int n) {
    int i;

    for (i = 0; i < n; i++) {
        InsertEndingElem(head, nums[i]);
    }
}

这个函数传入头指针，插入的数组首地址，数组个数，然后把数组中的元素以此插入到链表中。这里比较容易理解，遍历数组，依次调用插入函数即可。不过这里有个问题，因为每次调用插入函数时，都传入了 head 头指针，而每次调用后都要重新从 head 遍历到末尾，这就重复做了一些操作，可以思考一下怎么改进。

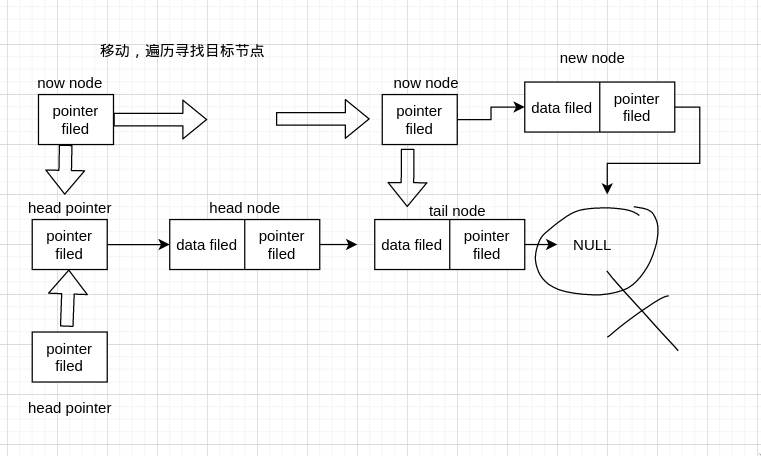
我们刚刚实现了在尾节点（tail node) 后插入 node，现在我们来看一下其他地方又怎么实现

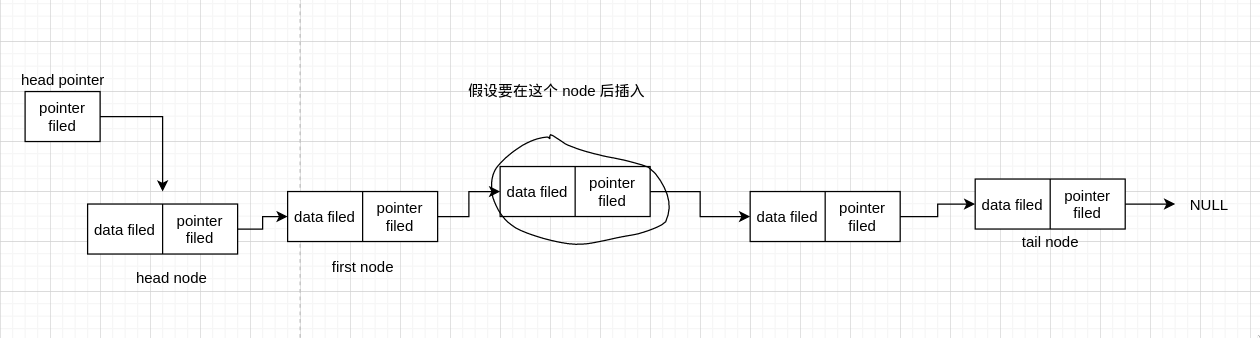
假设我们要在画圈的那个 node 后 insert 一个新的 node。同样的，我们需要 head pointer 记录开始的 node，需要一个当前节点 now_node 遍历到目标节点，然后插入节点，现在我们假设已经遍历找到了目标节点

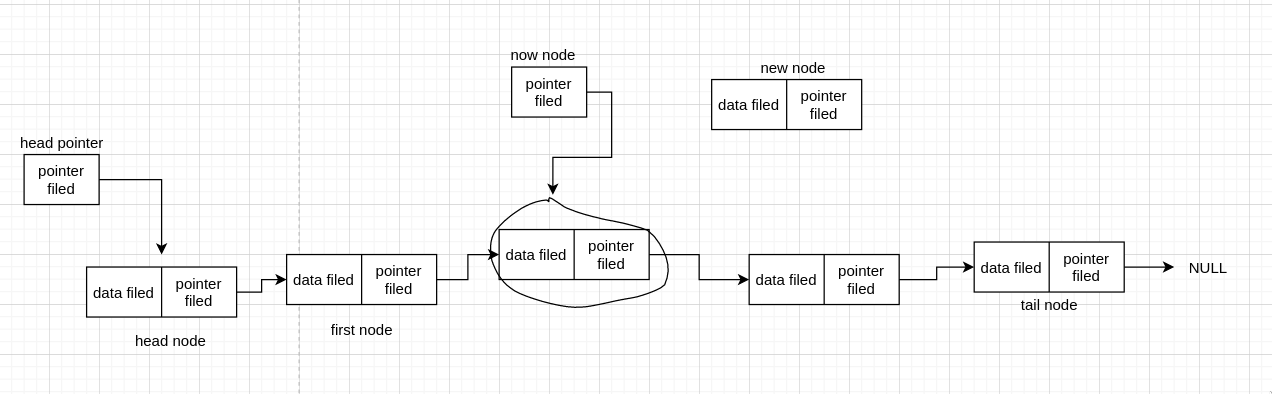
看图我们知道，要插入的话，只需把 now_node 和 new_node 连接起来，以及 new_node 和目标节点后面那个节点连接起来，也就是连两条线，那么先连哪条有区别吗？我们来看图

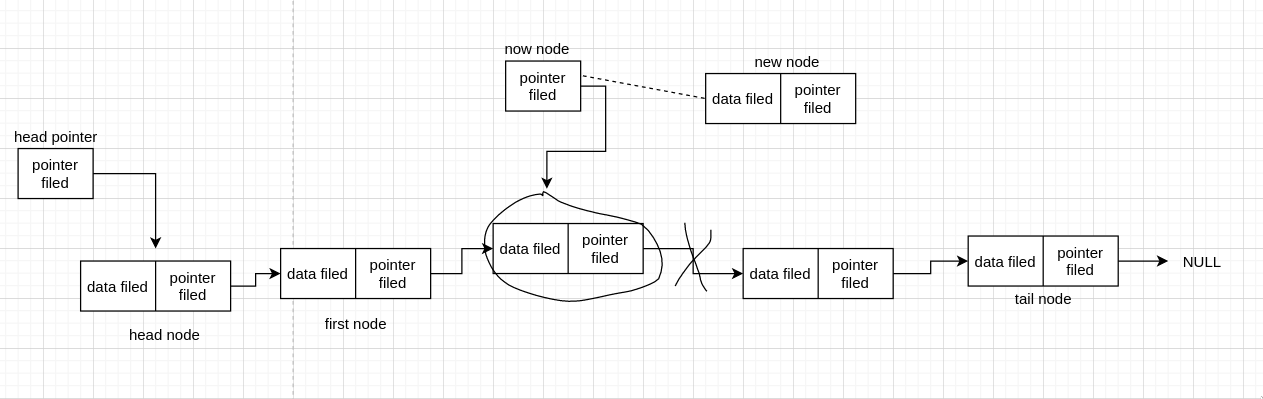
我们先连 now_node 和 new_node 这条线，我们知道 now_node 现在即目标 node (圈起来的 node)，于是目标 node 连接原先后面的那些 node 断了，因为连接到 new node 去了。现在我们继续，我们现在需要把 new node 连接到圈后面的那个 node，可是刚刚已经断开了，如果我们没有记录它的地址的话，我们就找不到这个 node 了。所以如果先连这条线的话，需要先保存目标 node 后面的 node address

我们来先连后面一条线看看

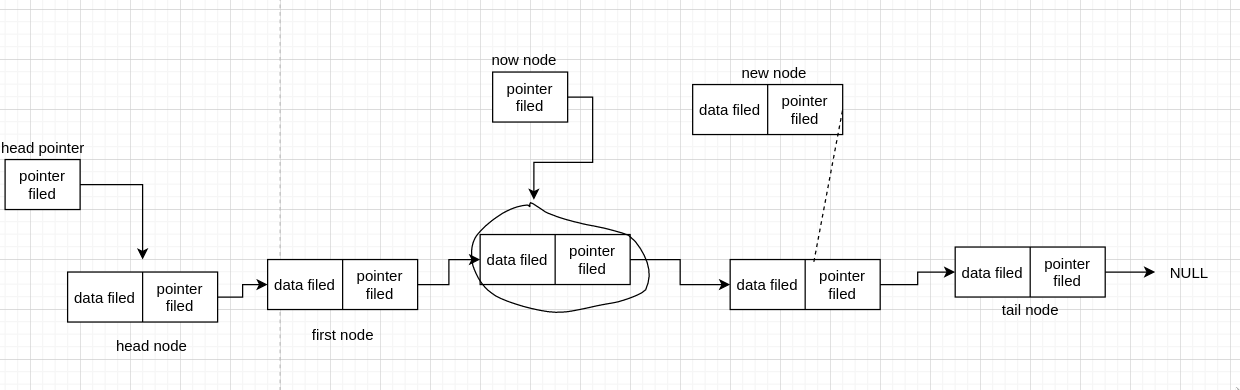
我们发现每个 node 都在，并没有丢失

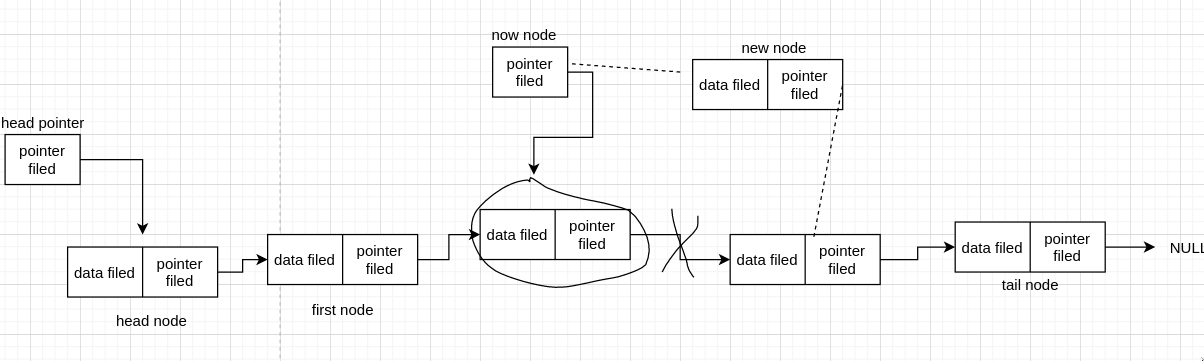
我们继续连第二条线，发现成功连上了，这说明我们成功插入了 node。

从上面的分析知道，虽然先连哪条线都能成功，但是先断后连的话，需要占用内存去存 node 的地址，而先连后断则没有这一步，故我们一般都是先连后断的。

通过上面的分析，我们发现，单链表要插入节点的话，只需更改一下 address 就可以了，其时间复杂度是 O(1)。

我们刚刚分析了原理，现在来具体用代码实现一下，要插入元素的话，首先需要找到插入点，而根据插入点的类型，又多种情况，如在第 n 后插入，在第一个 val 为 m 的 node 后插入，还有延伸插入 n 个元素等。不过这是查询节点的内容，以及扩展的部分，只要原理清楚了，其他再进行拓展是比较容易的。我们这里就假设插入的目标节点是第一个 data 为 m 的 node

// 在第一个 data 为 val 的 node 后插入一个 node，其值为 d
void InsertElemByValue(Node *head, int val, int d) {
    Node *now_node = head;  //遍历用的 node

	// 找到插入点
    while (now_node->data != val) {
        now_node = now_node->next;
    }
    // 插入的 node
    Node *New_node = (Node *) malloc(sizeof(int));
    New_node->data = d;
    // 插入，先连后断
    New_node->next = now_node->next;
    now_node->next = New_node;
}

这个函数在中间插入 node，首先遍历找到 data 为 val 的 node，然后建立好新 node，再用我们刚刚分析的，先连接，后断开的连线方式插入 node。

我们分析了插入中间，以及末尾的节点，现在我们再来看下在开始插入节点又是怎样的

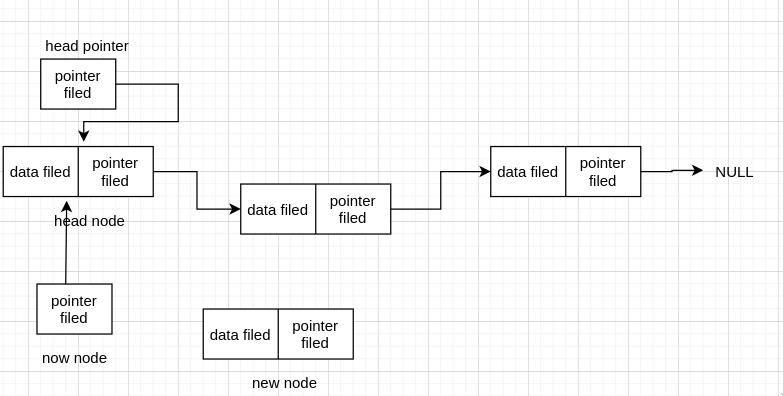
我们发现如果有头节点（head node) 的话，同样的头指针记录头节点，当前节点从头节点遍历。我们可以和在中间插入对比一下，细心一点我们会发现它们的过程是一样的，事实上我们也可以把这个当作在头节点后插入节点，这也是在中间插入的一种。所以有头节点的话，实现比较容易理解。

比如我们刚刚 InsertElemByValue() 函数, 如果 first node 的 val 值符合的话，那么是直接插入在 head node 后的，也就是插入第一个节点。

但是我们知道，还有没有头节点这种情况，那么这种情况又是怎么样的呢？

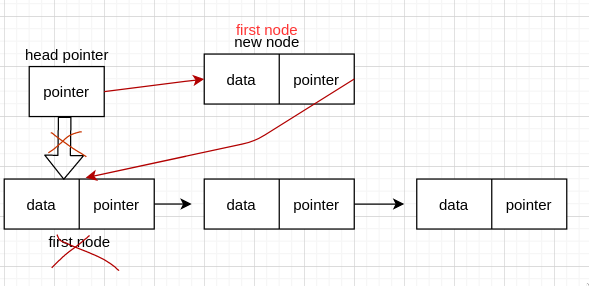
看图我们可以发现，由于没了 head node, 所以我们需要单独的设置，按照上面说的连续方式，我们需要先把 new node 连接到原先的 first node 上，然后把 head pointer 重新指向 new node。

我们来看一下代码

// 插入 fisrt node
void InsertNodeAfterHead(Node *head, int m) {
	// 建立 new node
    Node *new_node = (Node *)malloc(sizeof(int));
    new_node->data = m;

	//  插入
    new_node->next = head;
    head = new_node;
}

这个函数直接在 head pointer 后，first node 前插入一个 node。主要是插入的过程需要多加思考，先 new node 连线到要插入的 node 后的那个 node, 这里要插入的 node 不存在，所以是连接到 first node, 然后 head pointer 重新指向 new node(现在变成了 first node).

经过上面分析可以看出，如果有头节点的话，对头节点的操作和中间节点的操作是一样的，所以这也是我们一般要使用头节点的原因之一。

delete

linked list 的重难点就是 insert 和 delete element 的过程，我们现在再来看下 delete element 的过程是怎么样的。

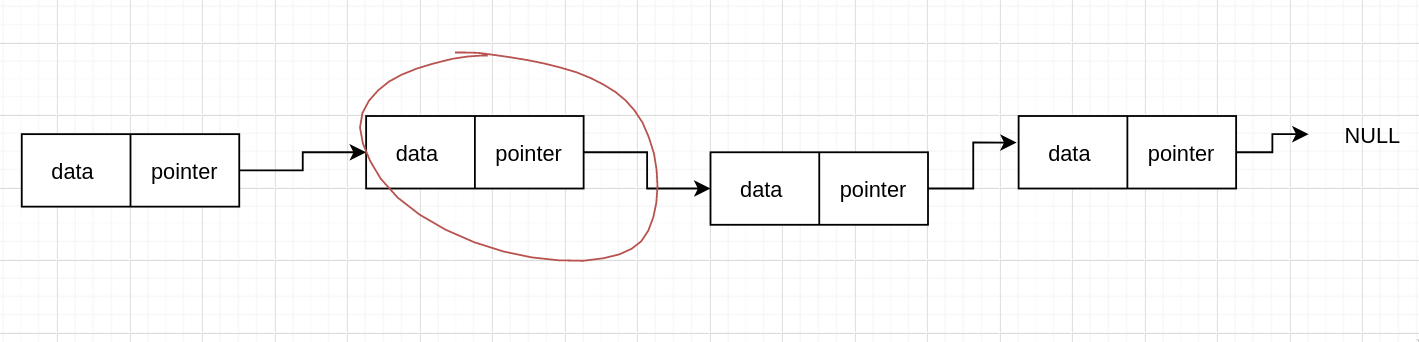
现在我们要删除圈起来的这个节点，怎么做呢？

我们知道链表中是使用指针将它们连接起来的，所以只需要不连接这个 node 就可以了，那我们可以直接找到前面那个节点，然后跳过这个节点

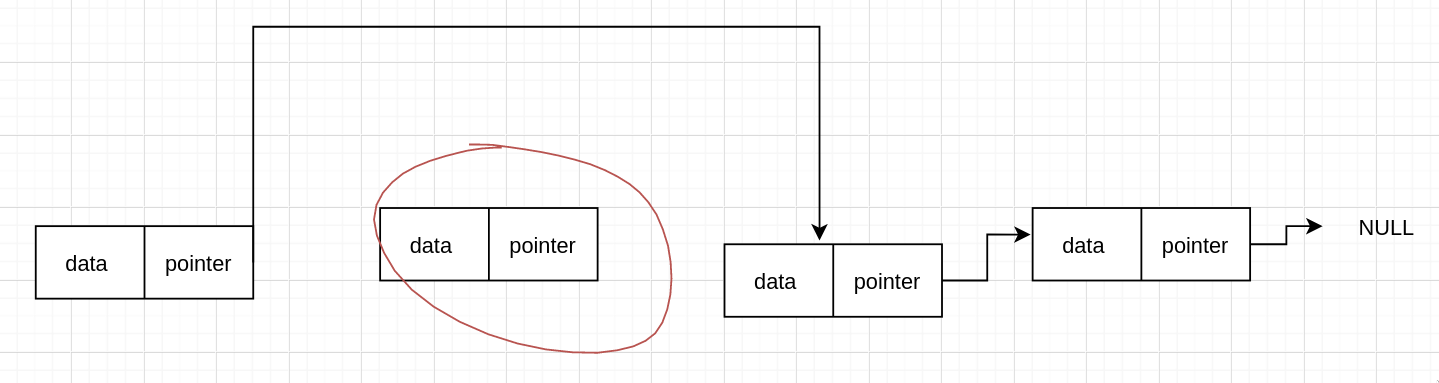
现在我们假设要删除第 n 个节点，所以需要先找到 n-1 个节点，然后跳过第 n 个节点，我们来看代码

// 删除第 m 个元素
void DeleteElem(Node *head, int m) {
	int i;
	Node *now_node = head;
	// 找到第 m - 1 个元素
	for (i = 0; i < m - 1; i++) {
		now_node = now_node->next;
	}
	// 删除元素
	now_node->next = (now_node->next)->next;
}

这个函数删除了第 m 个元素，先找到第 m - 1 个元素，然后删除这个元素。

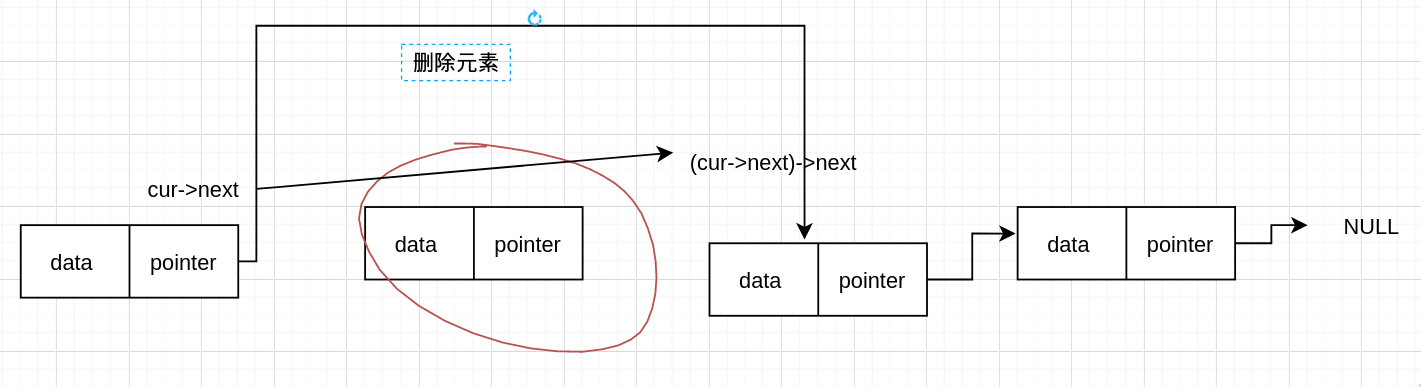
这里我们可以看到，删除的这个元素没有释放，那它占用的内存就被浪费了，这就发生了内存泄漏。我们可以先释放内存

// 删除第 m 个元素
void DeleteElem(Node *head, int m) {
	int i;
	Node *now_node = head;
	// 找到第 m - 1 个元素
	for (i = 0; i < m - 1; i++) {
		now_node = now_node->next;
	}
	// 先备份地址
	Node *temp = now_node->next;

	// 删除元素
	now_node->next = (now_node->next)->next;

	// 释放内存
	free(temp)
}

我们刚刚是删除了第 n 个元素，这种情况我们可以直接找到第 n 个元素，但是如果我们不知道要删除的元素位置呢？

如给一个值，然后删除值匹配的元素。这样的话我们就遍历匹配，但是只有当遍历到目标节点，才知道要删除的节点是那个，这样的话，除非我们保存了前面节点的地址，不然的话就不能像刚刚那种方法删除。

或者直接给一个 node，然后要你删除掉这个 node，这时候该怎么办？

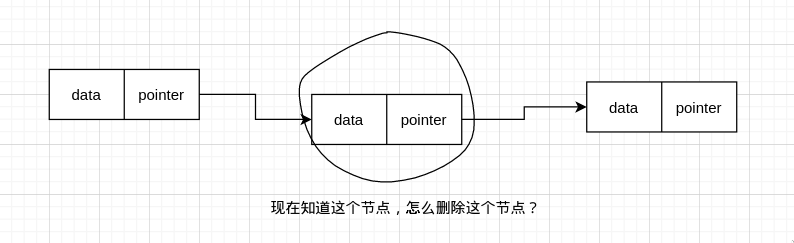
单链表只能往下遍历，不能往前遍历，所以这样是不行的

但是删除节点只能这样，我们现在只能这样

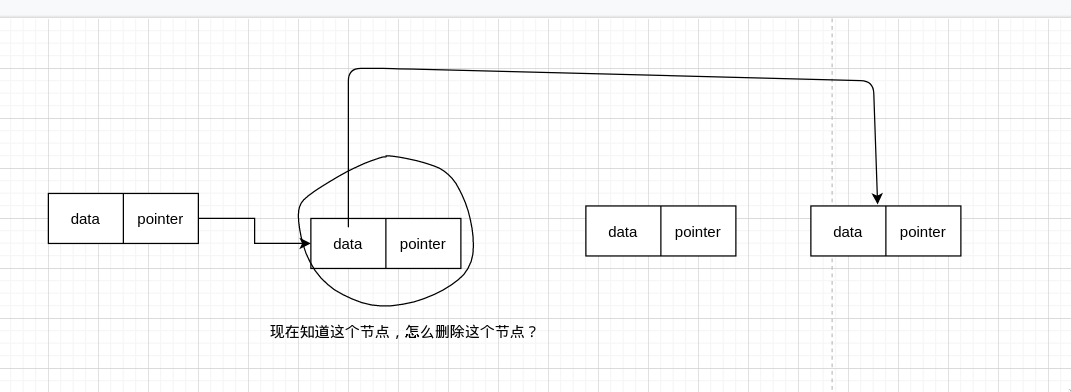
如果我们要删除的节点是后面这个就好了，等一下，既然如此，那我们只需要把要删除的节点变成后面这个不久好了？

假设原来的数据是这样的

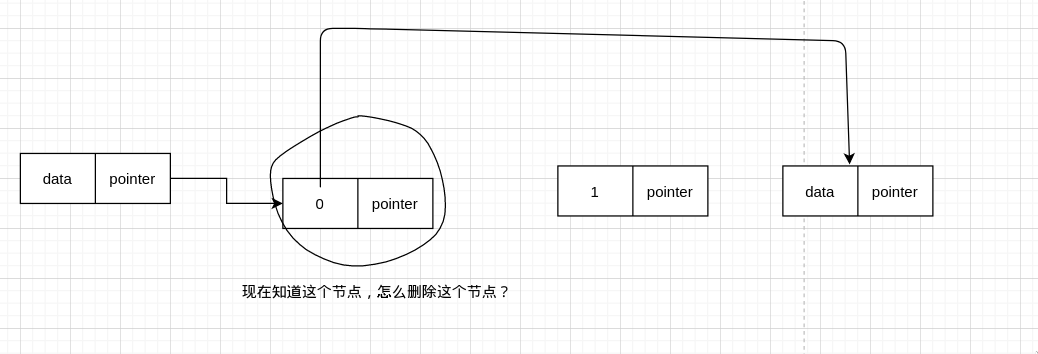
删除后是这样的

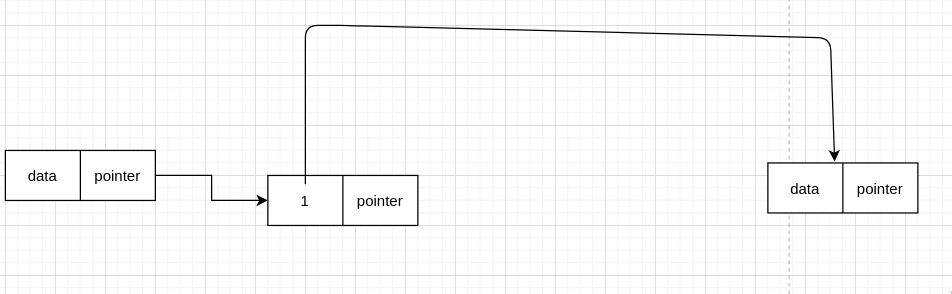
所以我们可以把圈起来那个节点的值，变成下一个节点的值

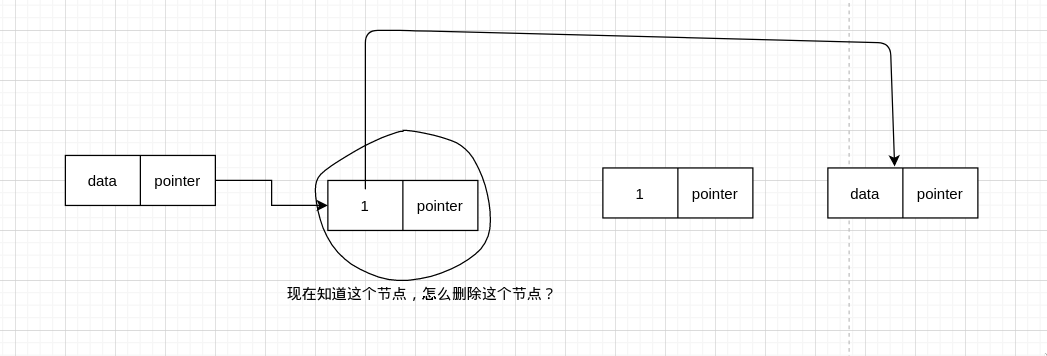
那我们要删除的节点就可以变成下一个节点

有人可能会说，可是它们的地址变了呀，对，是变了，但是我们只关心它们的值，地址是无需关心的。

我们来实现一下

void DeleteThisNode(Node *node) {
	// 复制值
	node->data = (node->next)->data;
	// 删除 node
	node->next = node->next->next;
}

这个函数删除了给定的这个 node，首先把删除的这个 node 的值变成下一个 node 的值，然后删除下一个 node。即把要删除的 node 变成下一个 node。

我们刚刚都是只删除了相邻的 node，我们也可以删除相邻的几个 node

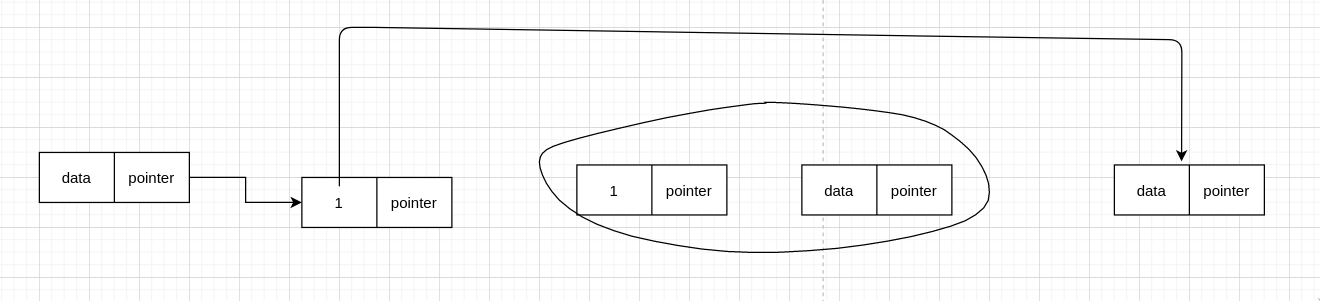
看图的话，知道原理其实都是差不多的

node->next = ((node->next)->next)->next;

当然还要释放一下内存，避免浪费。

上面都只删除了一个 node，当然我们也可以同时删除多个 node，如传入一个 array，然后删除里面的元素，或者删除多个值匹配的 node，这些都是在上面的基础上组合而成的，总之原理都差不多，这里就不展开了。

search

update

双链表

create

insert

delete

search

update

循环链表

单向循环链表

双向循环链表

静/动态链表

静态链表

静态单链表

静态单循环链表

静态双链表

静态双循环链表

动态链表

动态单链表

动态单循环链表

动态双链表

动态双循环链表

总结

参考

链表